人教版●三年级数学（上册）

第一题

1.秒　60　2.15　3:50　

3.4　10　4.120  300  145  3  90

第二题

秒　分钟　分钟　小时　

小时　秒　分钟　小时

第三题

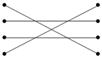
第四题

2　2　20　1　40　3　59

第六题

1.15　2.10

第七题

1.40分钟　2.9:30

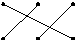
3.

第八题

1.小明晚上8时30分开始睡觉，睡了10小时。

2．分析：本题考查了学生对经过时间的理解与掌握以及应用速度、时间、路程的数量关系解决实际问题的能力。这道题关键在于求出小明一家开车所用的时间。只要求出经过时间，知道车的速度，就能求出这段时间内所行驶的路程。他们一家清晨5:00出发，想在上午9:00之前到达目的地。所经过的时间是9:00－5:00＝4（小时），而且汽车平均每小时行70千米，那么4小时所行驶的路程就是4×70＝280（千米）。题目中给出的小明家离合肥野生动物园有269千米。269＜280，所以他们在上午9:00之前能到达野生动物园。

解答：9:00－5:00＝4(小时) (2分)　4×70＝280(千米) (2分)　269＜280(2分)　

能到达。(1分)

第九题

分析：本题考查了学生根据已有的知识经验解决生活中与时间相关问题的能力。第1小题的解题关键在于理解王奶奶从1楼走到4楼一共走了几层，知道走一层楼所用时间，也就能求出从1楼走到4楼要用多少分钟了。根据生活经验，知道从1楼走到4楼需要走4－1＝3（层），而走一层楼要用2分钟，所以所用时间是2×3＝6（分）。第2小题的解题关键有两个：一是锯成2段要用3分钟，这是锯几次所用时间。没有锯过木头，可以撕一张纸，看撕成两半撕了几次，很明显这3分钟是锯1次所用时间；二是锯成9段是锯了几次得到的，通过刚才的方法进行多次实践可知，锯的次数＝锯成的段数－1，所以锯成9段是锯了9－1＝8（次），而一次需要3分钟，所以锯成9段需要3×8＝24（分）。第3小题是时间的优化问题。解题关键是这两件事哪件事是必须先做的，另一件事可以同时做。拖地和烧开水两件事，烧开水必须先做，在烧开水的同时可以拖地，所以，最少要用8分钟。

解答：1．6(4分)　2．24(4分)　3．8(4分)

第一题

1.22　22　18　

2.15　27　42  420  42  420

3.600

第二题

＜　＞　＞　＝ 　＝　＜

第三题

1.(竖排)61　80　9　200　770

79　48　97　250　270

2．470＋190＝660　　 560＋280＝840

320－140＝180　   　600－250＝350

3．220　171　348　500

第四题

340　700　310　270

第五题

分析：本题考查了学生自主收集信息解决问题的能力。题目中给出了三种物品的价钱。即：电话180元，椅子290元，电磁炉560元。要求把4个问题和4个算式连起来，那么只要把每一个问题列出算式，再和所给算式一一对应就可以了。第1个问题 “买一部电话和一把椅子一共要花多少钱？”求一共要花多少钱用加法计算，一部电话180元，一把椅子290元，所以，一共要花的钱数是180＋290＝470（元），与右边的第4个算式相连。第2个问题“买一把椅子和一台电磁炉一共要花多少钱？”同样要用加法计算，列式为290＋560＝850（元），与右边第1个算式相连。第3个问题“一台电磁炉比一部电话贵多少钱？”求谁比谁贵多少用减法计算，列式为560－180＝380（元），与右边第2个算式相连。第4个问题“一部电话比一把椅子便宜多少钱？”求谁比谁便宜多少也要用减法计算，列式为290－180＝110（元），与右边第3个算式相连。

解答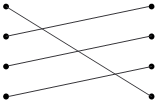：（8分）

第六题

1.(1)346－340＝6(米)

(2)340＋160＝500(米)

2．分析：本题考查了学生用估算解决生活中实际问题的能力。题目中一共给出了六件商品，围绕这六件商品提出了三个问题。（1）、（2）小题由问题中的“大约”两字可以确定为这是估算题。（1）小题“买一台电视机和一台吸尘器大约需要多少钱？”求买两件商品一共用的钱数要用加法计算，列式为788＋399，788可以看作是800，399可以看作是400，所以788＋399≈1200（元）。（2）小题“一部照相机比一台洗衣机贵86元，一部照相机大约多少钱？”两件商品比较，求较贵的商品，用加法计算，列式为509＋86，509可以看作是500，86可以看作是100，所以509＋86≈600（元）。（3）小题“妈妈带了1000元，她不可能同时买哪两样物品？”观察题目中所给物品价钱，有4种物品需要考虑，洗衣机509元，电视机788元，吸尘器399元，照相机595元。通过观察、估算，洗衣机509元＋电视机788元＞1000元，不能同时买；洗衣机509元＋照相机595元＞1000元，不能同时买；电视机788元+吸尘器399元＞1000元，不能同时买；电视机788元＋照相机595元＞1000元，不能同时买。

解答：(1)788＋399≈1200（元）(6分)　(2)509＋86≈600（元）(6分)

(3)她不可能同时买洗衣机和电视机或洗衣机和照相机或电视机和吸尘器或电视机和照相机。(6分)

第一题

1.10　1000　10

2．1

3．(1)千米　分钟　(2)吨　千克　(3)毫米

4．(1)大象　小狗　(2)68　(3)小狗　熊猫　大象

第二题

1.×　2.√　3. ×　4. ×　5. ×

第三题

1.4　2.5000　3.2　4.400　5.1　6.500　50　5

第四题

＜　＝　＞　＜　＜　＞

第六题

1.分析：本题考查了学生分析问题和解决问题的能力。解题关键是明确爸爸驾车2小时行驶了多少千米。爸爸驾车每小时行驶50千米，经过2小时就是行驶2个50，列式为50×2＝100（千米）。而明明家经过宜良到达石林的距离是65＋31＝96（千米），100＞96，所以经过2小时他们能从家经过宜良到达石林。

解答：50×2＝100(千米)(3分)　 65＋31＝96(千米) (3分)　100＞96　能到达。(1分)

2．分析：本题考查了学生思维的有序性、合理性以及学生应用已有知识进行推理的能力。由两位卡车司机的对话可以分析出四种卡车载质量的多少。第一个司机说“我的车载质量比轻型卡车多，比重型卡车少。”由此可见他的车是中型卡车或微型卡车；第二个司车说“我的车载质量比中型卡车少，比微型卡车多。”由此可见他的卡车是轻型卡车或重型卡车。通过图画上两车大小的比较，可知第一个司机的车是中型卡车，第二个司机的车是轻型卡车。中型卡车载质量＞轻型卡车载质量，而中型卡车载质量＜重型卡车载质量，轻型卡车载质量＞微型卡车载质量，所以，重型卡车载质量＞中型卡车载质量＞轻型卡车载质量＞微型卡车载质量。题目中给出了四辆卡车的载质量分别是6吨200千克、600千克、2吨500千克、8吨400千克，把这4个量按照从大到小的顺序进行排列，再与卡车的排序一一对应就可以了。因为8吨400千克＞6吨200千克＞2吨500千克＞600千克，所以重型卡车载质量为8吨400千克，中型卡车载质量为6吨200千克，轻型卡车载质量为2吨500千克，微型卡车载质量为600千克。

解答：(8分)

3．(1)400＋500＝900(米)　1千米＝1000米　1000－900＝100(米)

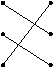
(2)

4．(1)16÷8＝2(元)　2×(8－2)＝12(元)

(2)8－2＋4＝10(吨)　2×10＝20(元)

5.分析：本题考查了学生解决问题时的优化思想。题目中给出了两种租船方式：一种是6人船8元一条，另一种是4人船5元一条。而一共有120人，想要最省钱的租船方案，就要算一算哪种租船方式花钱最少。用第一种租船方式要租几条船，花多少钱呢？一条船坐6人，有120人，就是看120里包含几个6，用除法计算，列式为120÷6＝20（条），而每条船8元，就是有20个8，用乘法计算，列式为20×8＝160（元），所以用第一种方式租船需要160元。用第二种租船方式又要租几条船，花多少钱呢？一条船坐4人，有120人，就是看120里包含几个4，用除法计算，列式为120÷4＝30（条），而每条船5元，就是有30个5，用乘法计算，列式为30×5＝150（元），所以用第二种方式租船需要150元。160＞150，所以租4人船5元一条最省钱。

解答：租6人船8元一条：120÷6=20（条）　20×8=160（元）(4分)

租4人船5元一条：120÷4=30（条）　30×5=150（元）(4分)

160＞150　租4人船5元一条最省钱。(1分)

第一题

1.1098　900　2.减少　

3.812　4.228　

5．200　6.＞　＜　＝　7.214　51

第二题

1.C　2.A　3.C　4.A　5.C

第三题

803　463　801　159

第四题

1.906－346＝560(万平方千米)

2．197＋208＝405(个)　405＜436　能坐下。

3．(1)273＋128＝401(元)

(2)456－278＝178(元)

(3)62＋456＝518(元)　518＞500　不够。

518－500＝18(元)

4．分析：本题考查了学生分析问题和解决问题的能力。题目中给出了三种节水措施，可有效地节省标准煤的用量。第一种是由盆浴改为淋浴，全国每年可节能约574万吨标准煤，第二种是洗澡时及时关闭水龙头，全国每年可节能约210万吨标准煤，第三种是避免水龙头漏水，全国每年可节能约340万吨标准煤。问题（1）通过以上三种节水措施，全国每年可节能约多少万吨标准煤？实际上就是求一共节约的标准煤量，用加法计算，列式为574＋210＋340＝1124（万吨）。问题（2）是选择算式574＋210－340的意义，算式中574是改用淋浴所节约的标准煤量，210是洗澡时及时关闭水龙头节约的标准煤量，两个数相加就是合理洗浴所节约的标准煤量，而340是避免水龙头漏水节约的标准煤量，所以这个算式表示的意义是合理洗浴所节约的标准煤比避免水龙头漏水节约的标准煤多多少万吨。

解答：(1)574＋210＋340＝1124(万吨) (8分)

(2)B(8分)

第五题

分析：本题考查了学生对综合运用加、减法计算知识的掌握情况以及学生的推理能力。第1小题是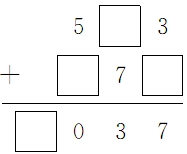，从个位入手，3＋□＝7，可知个位上的□里填4；十位上是□＋7＝3，通过口算，可知6＋7＝13，要向百位进1，十位上的□里填6；百位上5＋□＝□0，这里可以先确定和的千位上是1，百位上5＋□＝10，且要考虑到十位上6＋7＝13，向百位进1了，所以百位上的□里填10－1－5＝4。因此，第1个算式应填为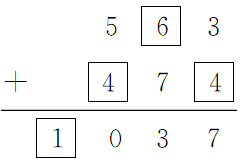。第2个算式是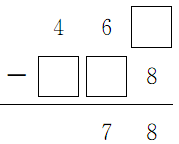，同样从个位入手，个位上□－8＝8，属于退位减法，因为16－8＝8，所以个位上的□里填6，且十位上数字6退1为5；十位上改为5－□＝7，又是退位减法，百位上数字4退1，十位上再次改为15－□＝7，因此，十位上的□里填8；而百位上数字4已退1，百位上就为3－□＝0，所以百位上□里填3。因此，第2个算式应填为。

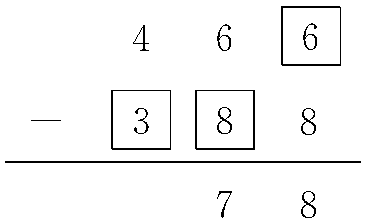解答：(8分)　 (6分)

第一题

1.0　2.四　3.627　870　

4.1800　5.1　0　6.2820　

第二题

1.2400　1800　1200　2000

2．389×8＝3112　　　　606×6＝3636

980×7＝6860　　　　　840×5＝4200

第三题

分析：本题考查了学生对多位数乘一位数算法的理解与掌握情况。（1）340乘5的积的末尾有1个0。这句话是错误的。因为340×5＝1700，积的末尾有2个0，而不是1个0，所以这句话错误。（2）积的末尾有0的算式，因数的末尾一定也有0。这句话是错误的。例如：215×2，因数的末尾没有0，而215×2＝430，积的末尾却有1个0，所以这句话错误。（3）108×9的积是三位数。这句话是正确的。108×9＝972，积是三位数。（4）两个数相乘的积一定比这两个数的和大。这句话是错误的。例如：1×1＝1，1＋1＝2，1＜2，所以这句话错误。再例如：2×2＝4，2＋2＝4，4＝4，所以这句话错误。

解答：1. ×(2分)　2. ×(2分)　3.√(2分)　4. ×(2分)

第四题

1.分析：本题考查了学生对多位数乘一位数的积的末尾有0的计算方法的理解与掌握情况。305×8＝2440，积的末尾有1个0，故选择A。

解答：A(2分)

2.B(2分)

3.分析：本题考查了学生的思维能力和推理能力。题目中给出1□×7这个算式，同时要求积是两位数，那么□里最大能填几呢？按进位乘法来想，□×7不能大于或等于30，因为7加进位3会向百位进一，积就是三位数了。因为4×7＝28，小于30，所以□里最大能填4，故选择C。

解答：C(2分)

4.C(2分)　5.A(2分)

第五题

1.708×5＝3540(万吨)

2．195×3≈200×3＝600(元)　195＜200　带600元够。

3．37×8－7＝289(年)

4.分析：本题考查了学生对倍数含义的理解以及发现问题和提出问题的能力。题目中给出了美术小组和书法小组的人数，而且还给出“合唱小组的人数是美术小组和书法小组人数和的2倍，”根据这句话可以提出问题：合唱小组有多少人？要解答这个问题，关键是要知道合唱小组的人数同谁有关系。因为合唱小组的人数是美术小组和书法小组人数和的2倍，所以要先求美术小组与书法小组的人数和，列式为42＋58＝100（人），而求一个数的2倍是多少，用乘法计算，列式为100×2＝200（人）。

解答：合唱小组有多少人(3分)

42＋58＝100（人）　100×2＝200（人）(3分)

5．(1040＋168)×2＝2416(个)

6．35÷7×180＝900(吨)

第六题

1.分析：本题考查了学生的探究与推理能力。题目中提示了要用中间数936与一个数相乘得到“和”。通过观察发现，933＋939是2个936的和，934＋938是2个936的和，935＋937是2个936的和，再加上1个936，一共有7个936，所以933＋934＋935＋936＋937＋938＋939＝936×7＝6552。

解答：　

933＋934＋935＋936＋937＋938＋939

＝936× 7

＝(6552) (4分)

2．分析：本题考查了学生逆向思考一位数乘整百数的乘法算式以及有序思考的能力。题目要求写出积是2400的一位数乘整百数的算式。因为其中有一个因数是整百数，所以只要思考哪两个因数相乘等于24就可以了。因为1×24＝24，2×12＝24，3×8＝24，4×6＝24，其中1×24，2×12不符合题目要求，所以符合要求的算式是300×8＝2400，3×800＝2400，400×6＝2400，4×600＝2400。

解答：300×8＝2400　3×800＝2400　400×6＝2400　6×400＝2400(6分)

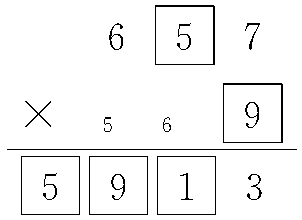
3.分析：本题考查了学生对三位数乘一位数计算方法的掌握以及推理能力。1小题为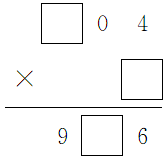，计算时从个位乘起。要先考虑4×□＝6，通过口算知道4×4＝16，要向十位进一，而□里填4；十位上0×4＝0，再加进位的1，等于1，所以积的十位上的□里填1；百位上□×4＝9，这里没有任何数乘4等于9，所以，前面思考错误，要重新填写。那么，就要再思考除了4以外，还有哪个数字与4相乘，个位上是6，通过口算知道4×9＝36，所以第二个因数是9。4×9＝36，要向十位进三，而十位上0×9＝0，0＋3＝3，所以，积的十位上的□里填3；百位上□×9＝9，可知□里应填1。所以，1小题填后应是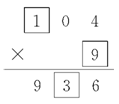。2小题为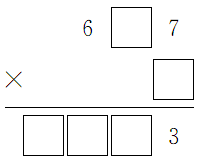，同样要从个位乘起，个位7×□＝3，想要7×□个位上是3，通过口算可知7×9＝63，所以□里填9，也就是第二个因数是9；再用第一个因数十位上数字□×9，因为积是四位数，而且千位、百位、十位上的数字不确定，所以□里的数字可以填写0~9中的任意数字；再根据第一个因数十位上数字的填写来确定积千位、百位、十位上的数字。如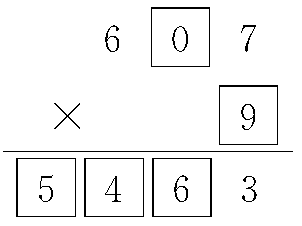　（答案不唯一）

解答：(3分)　  (5分) (后一题答案不唯一)

第一题

1.30　2.4　2　12　3.20

第二题

1.B　2.A　3.C　4.D　5.C

第三题

1.96米　2.32分米　3.650分米

第四题

1.2　2.20　3.16

第五题

1.357＋357＋178＋178＝1070(厘米)

1070＋1070＝2140(厘米)

2．9×4＝36(厘米)

3．(1)2　(2)15×4＝60(厘米)

4．(1)B　(2)女孩√

5．分析：本题考查了学生综合运用已学的周长、长方形的特性等知识解决生活中简单问题的能力。题目中给出了小明从家到奶奶家的三条路，通过对所给图形的观察与分析，知道走第1条路要走60＋80＝140（米），走第2条路要走100米，第3条路把线段还原一下，会发现它和第一条路同样长，都是长方形一个长与一个宽的和，即60＋80＝140（米）。因为140＞100，所以走第2条路最近。140－100＝40（米），走第3条路比走第2条路多走40米。

解答：(1)走第2条路最近。(5分)

(2)60＋80＝140(米) (5分)

(3)140－100＝40(米) (5分)

6．分析：本题考查了学生对长方形、正方形周长的认识与理解以及对较复杂图形周长计算方法的掌握情况。观察题目中所给图形可知，一个正方形被两条线段分成4个长方形，而且4个长方形的周长和是16分米，求原来正方形的周长是多少分米。由图形来看，首先这4个长方形外围的一圈正好是正方形的周长，那么里面线段的长度和又是多少呢？我们通过平移，画图来看一看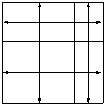：，发现将4个长方形里面这几条线段平移到外面边框，就又是一个正方形的周长。所以，这4个长方形周长和里共含有2个正方形的周长，因此一个正方形的周长是16÷2＝8（分米）。

解答：16÷2＝8(分米)(9分)

第一题

1.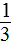　三分之一

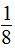2.　3

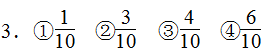
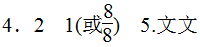
第二题

1. ×　2. ×　3.√　4. ×　5. ×

第三题

1.B　2.A　3.B

第四题

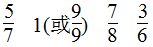
第五题

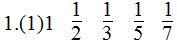
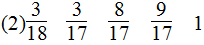
2．＞　＜

第六题

1.3　2　2. 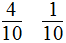　　小猪　小兔

第七题

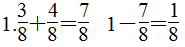
2．分析：本题考查了学生对分数含义的理解以及对分数加减法的掌握。

（1）小题根据题意，解题关键是要把湖北省鄂州市图书馆持证读者1万人看作1个整体。因为16岁以下的少年读者占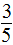，60岁以上的老年读者占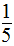，那么，其他年龄段的读者占持证读者总人数的几分之几，可以用减法计算。列式为1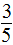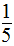－－，这里的“1”可以用分数来表示，所以1－－＝－－＝。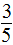

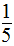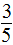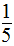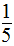（2）小题是要求根据算式提出问题并解答。所给算式是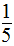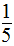＋。根据题目中所给已知条件和问题（1）的解答，可知这两个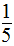分别是指60岁以上的老年读者占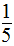和其他年龄段的读者占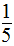，加在一起求的就是60岁以上的老年读者和其他年龄段的读者共占持证读者总人数的几分之几？＋＝。

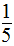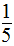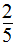解答：(1)1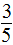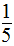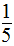－－＝(6分)

(2)60岁以上的老年读者和其他年龄段的读者共占持证读者总人数的几分之几？

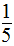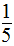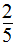＋＝(6分)

3．分析：本题考查了学生对集合的含义与运算的掌握及用集合的思想方法解决简单的实际问题的能力。题目中用统计表给出了三（2）班同学获得优秀书法奖和优秀作文奖的学生名单，在填写集合图时，为避免出现错误，先要把两项都获奖的名字填入交集圈里，再把其他学生的名字填入相应的集合圈里。要想求获得优秀书法奖和优秀作文奖的一共有多少人？要把两个集合中的人数相加再减去交集圈里的人数。即8＋8－3＝13（人）

解答：（1）(6分)

(2)8＋8－3＝13(人) (6分)