四年级数学（上册） - 五 平行四边形和梯形
1．平行与垂直
第1题
（1）○ （3）△ （6）△ （8）○
第2题
（1）
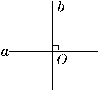b⊥a b垂直于a
（2）a∥b a平行于b
第3题
（1）A （2）C （3）B
第4题
分析：①在同一平面内不相交的两条直线叫平行线，也可以说这两条直线互相平行。
②如果两条直线相交成直角，就说这两条直线互相垂直。
根据上述两个定义我们可判断出。
①a∥b或b∥a d∥e或e∥d g∥f或f∥g
②g⊥a b⊥g f⊥a b⊥f
解答：互相平行：a∥b或b∥a、d∥e或e∥d、g∥f或f∥g……（3分）
互相垂直：g⊥a、b⊥g、f⊥a、b⊥f……（4分）
第5题
分析：①在同一平面内不相交的两条直线叫平行线，也可以说这两条直线互相平行。
②如果两条直线相交成直角，就说这两条直线互相垂直。
如图，根据定义可以判断出：
①AD∥BC或BC∥AD、AB∥CD或CD∥AB，共2组；
②DE⊥AC、AB⊥BC、BC⊥CD、CD⊥DA、
DA⊥AB，共5组。
解答：2 5
2．垂线的画法
第1题
（1）× （2）√
第2题
（2）
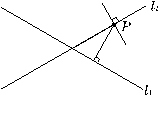
第3题
（1）B （2）A
第4题
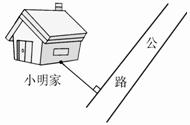
第5题
分析：要想使把清理出的污物送到岸上路线划行最短，首先要走垂直的路线，因为两点之间垂线段最短。再看离哪个方向的岸边近，就向哪个方向的岸划船。
解答：如图：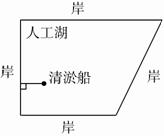
第6题
分析：题中没有要求玻璃的形状，只要将正方形分成相等的四份就可以了。
解答：如图：
（方法不唯一）
3．解决问题
第1题
（1）√ （2）√ （3）√
第3题
分析：此题适合按要求动手实际操作。
解答：正方形
第4题
（1）（画法不唯一）
（2）不能
第5题
分析：通过观察给出的图形发现：①一定为正方形，因为露出的完整的两条边长度相等；②一定为长方形，因为露出的完整的两条边长度不相等；③一定为长方形，因为露出的两条平行边长度均比第三条完整的边长；不能确定是长方形还是正方形的是④，④既可能是正方形，又可能是长方形。
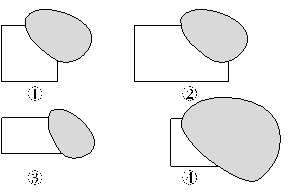
解答：（1）②、③号图形。
（2）①号图形。
（3）④号图形既可能是正方形，又可能是长方形。
4．平行四边形和梯形(1)平行四边形的认识
第1题
（1）相等 相等 180°
（2）5厘米
第2题
①④
第3题
（1）C （2）A
第4题
明明（√） 方方（√）
第5题
（1）× （2）×
第6题
10 7
第10题
分析：平行四边形两组对边分别平行且相等，把每条边平均分成两份，再把对边的中点用虚线连起来。
解答： 方法一 方法二
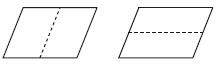
第11题
平行四边形易变形的特性。
第12题
分析：两组对边分别平行的四边形叫平行四边形。通过观察可以判断出：平行四边形有：平行四边形ABGF，平行四边形BFGD，平行四边形CFGE，我们发现这些平行四边形有相同的底，高也相等。
解答：找到三个平行四边形。这些平行四边形同底等高。
第13题
分析：如图，平行四边形的特点是两组对边分别平行且相等，13米对应的边长也是13米，另两条边的长度为2a米，已知平行四边形的周长是42米，即13×2+2a＝42，求得a＝8，也可以用（42－13×2）÷2＝8（米）求得。
解答：设平行四边形的另一条边长为a米。……（2分）
13×2+2a＝42……（6分）
a=8
答：平行四边形另外三条边长分别是13米、8米、8米。……（2分）
第14题
分析：根据平行四边形的定义来判断一共有多少个平行四边形。
通过数一数可知，共有9个平行四边形。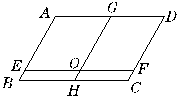
分别是平行四边形AEOG、平行四边形EBHO、平行四边形ABHG、平行四边形GOFD、平行四边形OHCF、平行四边形GHCD、平行四边形AEFD、平行四边形EBCF、平行四边形ABCD。
解答：9个
4．平行四边形和梯形(2)梯形的认识及四边形之间的关系
第1题
（1）一组 上底 下底 垂直线段 （2）两腰 直角
第2题
（1）√ （3）√ （5）√ （6）√
第3题
（1）√ （2）× （3）× （4）√ （5）×
第5题
第7题
B
第8题
下底和高都是6厘米。
第9题
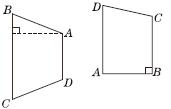
分析：只有一组对边平行的四边形叫梯形。按照定义判断，如图（1），图中的梯形有3个，分别是梯形ABFE、梯形FCAD、梯形DECB。
按照定义判断，如图（2），图中的梯形有梯形GEDA、梯形HFDB、梯形BHFG、梯形EFCB，共4个。
解答：3 4
第11题
分析：（1）把河岸作为梯形的上底，围这块菜地需要篱笆：
13+7+7＝27（米）
（2）把河岸作为梯形的下底，围这块菜地需要篱笆：
5+7+7＝19（米）
（3）把河岸作为梯形的一条腰，围这块菜地需要篱笆：
13+5+7＝25（米）
比较以上三种围法，判断出张大爷采用了（2）的围法。
解答：（1）13 7 7 27
（2）5 7 7 19
（3）13 5 7 25 （4）（2）