五年级数学(上册) - 三 小数除法
1.除数是整数的小数除法
第1题
(1)2.5 10 10 25
(2)3.4 10 10 34
第2题

第3题
分析:(1)此题错在说法不严密。应该是一个小数除以大于1的整数,商一定小于这个小数。
(2)被除数是小数,且小数的整数部分小于除数,得到的商一定比1小。此题被除数的整数部分是5,5小于6所以商比1小这种说法是对的。
(3)此题的说法是正确的。
解答:(1)×(2)√(3)√
第4题
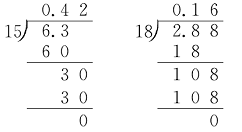
第5题
0.86 0.51 0.96 0.52
第6题
分析:(1)从表格上看所得的商都是相同的,所以被除数和除数同时扩大相同的倍数时,商不变。
(2)根据 “被除数和除数同时扩大相同的倍数商不变”,0.72÷0.8的被除数和除数同时扩大10倍,转化成7.2÷8,商是0.9。
解答:填表如下:

(1)不变
(2)0.9
第7题
(86.1-84.9)÷6×15=3(元)
第8题
8.8÷4=2.2(元)
12.5÷5=2.5(元)
12.6÷6=2.1(元)
2.1<2.2<2.5 第三种笔比较便宜。
第9题
分析:(1)一个小数的小数点向右移动一位是把这个小数扩大到原来的10倍。假设丽丽的计算结果是a,那么明明把这个计算结果扩大10倍就是10a,比原来多了9a ,明明的计算结果比丽丽的计算结果多45.72,45.72就是多的9a,求出a是多少即可。用线段图表示更加清晰。如图:
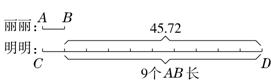
由上图可知,明明的计算结果比正确的计算结果增加了9倍。
(2)明明的计算结果比正确的计算结果增加了9倍,也就是正确的计算结果的9倍是45.72,45.72÷9得到的商就是正确的计算结果。
(3)一个小数的小数点向右移动两位,就是把这个小数扩大到原来的100倍。假设这个小数是a,那么把这个小数扩大100倍就是100a,比原来多了99a ,结果比原来增加的346.5就是多的99a,求出a是多少即可。
解答:(1)10 9
(2)45.72÷(10-1)=5.08
(3)346.5÷(100-1)=3.5
2.一个数除以小数
第1题
(1)3.1 (2)10 9 6.1 10
(3)104 26 4
第2题
(1)B (2)A
第3题
600 16800 28 600 25 350 14 25
第4题
70 290 2.88 40
第5题
第6题
> < > =
第7题
5.46÷0.70=7.80(分)
25.20÷7.20=3.50(分)
7.80>3.50 红红的通话时间长。
第8题
12240÷6.12=2000(美元)
第9题
50÷2.5=20(支)
第10题
分析:把宁宁钱数的小数点向左移动一位就是把这个数缩小到原来的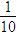 ,正好和丽丽的钱数相等,也就是宁宁的钱数是丽丽钱数的10倍。
,正好和丽丽的钱数相等,也就是宁宁的钱数是丽丽钱数的10倍。
用线段图表示如下:

从上图可以看出丽丽钱数的11倍是61.6元,即可求出丽丽有多少钱。丽丽的钱数再乘10就是宁宁的钱数。
解答:61.6÷(10+1)……3分
=5.6(元)……2分
5.6×10=56(元)……2分
答:宁宁有56元,丽丽有5.6元。……1分
第11题
(1)分析:
①47.94÷9.4=5.1。小数点左边的数是5,右边的数是1,也就是5月1日,5月1日是国际劳动节。
②20.14÷5.3=3.8。小数点左边的数是3,右边的数是8,也就是3月8日,3月8日是妇女节。
③57.57÷5.7=10.1。小数点左边的数是10,右边的数是1,也就是10月1日,10月1日是国庆节。
④2.257÷0.37=6.1。小数点左边的数是6,右边的数是1,也就是6月1日,6月1日是儿童节。
解答:①47.94÷9.4=5.1 国际劳动节
②20.14÷5.3=3.8 妇女节
③57.57÷5.7=10.1 国庆节
④2.257÷0.37=6.1 儿童节
第12题
分析:小明花车费12.5元,去掉3 km以内的5元,剩7.5元,每千米1.5元,7.5元最多可以行驶7.5÷1.5=5( km),那么小明家距奶奶家最远有5+3=8(km)。
解答:12.5-5=7.5(元)……3分
7.5÷1.5=5(km)……4分
3+5=8(km)……3分
答:小明家距奶奶家最远有8千米。……1分
3.商的近似数
第1题
(1)5.724 5.715 (2)百分 千分
第2题
(1)B (2)A (3)C (4)C (5)A
第3题
分析:(1)首先计算出1÷6的结果是0.1666…,精确到百分位就是精确到小数点后第二位。此题错在精确到了小数点后第3位,也就是千分位。
(2)根据“四舍五入”法求近似数时应除到比要保留的位数多一位。所以此题是正确的。
(3) 8.00精确到的是百分位,而8.0精确到的是十分位,小数末尾的0去掉后,数的精确值就变了,因此本题的叙述不正确。
解答:(1)×(2)√(3)×
第4题
15.5 17.4 0.2 13.6
第5题
1.90 7.87
第6题
36.69÷13.6≈3
第7题
15000÷127≈118(个)
【※浙江专用】7. 567÷90≈6(平方千米)
第8题
125.8÷12≈10.5(t)
第10题
1000000÷365÷24≈114(人)
第11题
分析:(1)“四舍五入”后的近似数是4,就是精确到整数,那么这个小数的整数部分不是3就是4,所给的数字只有4符合条件,那么十分位上的数就只能舍去,所以符合条件的只有0,6和9只能放在百分位和千分位上。所以可以组成两个符合条件的小数,即4.069和4.096。
(2)要想“四舍五入”后的近似数小于1,那么整数部分必须是0,而且十分位上的数必须小于5,所以十分位上的数只能是4 ,6和9只能放在百分位和千分位上。所以可以组成两个符合条件的小数,即0.469和0.496。
解答:(1)4.069 4.096 (2)0.469 0.496
4.循环小数
第1题
(2)①9.358 ②6.103
第2题
分析:(1)此题是错的,这个小数的循环节是7215,简便记法是在这个循环节的首位和末位数字上面各记一个圆点。正确写法是5.37215。
(2)此题是错的,除不尽时得到的商还可能是无限不循环小数。
(3)此题是错的,3.34646不是循环小数,没有循环节。
(4)此题是对的,2÷6的商是0.3333…,商是循环小数。
(5)此题是错的,有的循环小数大于1,如3.555…。
解答:(1)×(2)×(3)×(4)√(5)×
第3题
分析:(1)把题中的每个循环小数都展开,再进行比较。
9.808=9.808808…
9. 808 =9.808
9.808=9.80808…
9.808=9.808888…
这4个小数的整数部分都是9,小数点后三位都是808,所以从小数点后第四位开始比较。9.808的小数点后第四位是8,而A选项和B选项的小数点后第四位都是0,因此排除A选项和B选项;C选项小数点后第四位是8,因此比较9. 808和9.808的小数点后第五位,9.808的小数点后第五位是0,而9.808的小数点后第五位是8,8>0,即9.808>9.808,所以C选项符合条件。
(2)由于4个小数的整数部分都相同,所以首先比较小数点后第一位,B选项小数点后第一位是4,0.34小数点后第一位是3,4>3,首先排除B选项;再比较小数点后第二位,A选项、C选项和0.34小数点后第二位都是4,所以接着比较小数点后第三位,A选项小数点后第三位是4,C选项小数点后第三位是3,0.34小数点后第三位是3,因此排除A选项; C选项小数点后第四位是3,0.34小数点后第四位是4,4>3,所以正确答案是C。
解答:(1)C (2)C
第4题
> < > < < <
第5题
分析:(1)此题是错的。8.53保留两位小数就要看小数点后第三位,小数点后第三位是5,需要向前一位进1,所以8.53保留两位小数应是8.54。
(2)此题是错的。无限小数包括无限循环小数和无限不循环小数。
(3)此题是对的。一个小数不是有限小数就是无限小数。
(4)此题是错的。比较小数的大小不能只看小数的位数,要从最高位开始比较。
(5)此题错在说法不严密。正确的说法是小数部分从某一位起,一个数字或者几个数字依次不断地重复出现,这样的小数叫循环小数。
解答:(1)×(2)×(3)√(4)×(5)×
第7题
4.2 0.6 3.136 0.34
第8题
630÷7.3≈86(km)
【※浙江专用】8.2008÷3.347≈600(m3)
第9题
分析:要想知道第73个字是什么,要根据73除以4的余数来确定。如果没有余数,第73个字就是“华”;如果余数是1,第73个字就是“爱”;如果余数是2,第73个字就是“我”;如果余数是3,第73个字就是“中”。
解答:73÷4=18(组)……1(个)……6分
答:明明写的第73个字是“爱”。 ……1分
第10题
200÷3≈66.67(kg)
第11题
分析:解答本题的关键是明确彩灯的排列顺序。彩灯按3盏红灯、4盏绿灯、2盏黄灯的顺序挂,可以把这3+4+2=9(盏)彩灯看作一组,用除法计算出1000盏彩灯中有多少个这样的一组,再根据余数确定第1000盏彩灯的颜色。 1000÷9=111(组)……1(盏),即有111组这样的彩灯还余1盏,这1盏就是一组中的第1盏,即红灯。
解答:1000÷(3+4+2)=111(组)……1(盏)……8分
答:第1000盏彩灯是红色的。……1分
第12题
分析:循环小数7.2306306…是从小数点后第二位开始循环的,它的循环节是306,周期是3,要想知道它的小数部分第10位和第2015位是几,就要用除法计算出前10位和前2015位中有多少个周期,再根据余数来确定。要求小数部分第10位是几,要把小数部分第一位不是循环节中的2去掉,还剩9位,9÷3=3(组),没有余数,那么小数部分第10位就是循环节中的最后一个数字6。要求小数部分第2015位是几,要用2015减1得2014,2014÷3=671(组)……1(个),余数是1,那么小数部分第2015位就是循环节中的第一个数字3。
解答:(10-1)÷3=3(组)……5分
(2015-1)÷3=671(组)……1(个)……5分
答:它的小数部分第10位是6,第2015位是3。…1分
5.用计算器探索规律
第1题
40 12 4.16875 24.75 1.26 5.5
第2题
63 66.33 666.333 6666.3333
66666.33333 666666.333333
6666666.3333333
第3题
(1)1.234321 1.23454321 1.2345654321
(2)555555 666666 777777 7999992
888888 8999991 999999
第4题
分析:
(1)计算前三个算式的商:
2.88÷9=0.32
3.798÷9=0.422
4.6998÷9=0.5222
观察上面三个算式,除数都是9,而被除数和商同时发生变化。先观察被除数的变化规律,从2.88开始,整数部分逐次增加1,小数部分的位数逐次增加1,十分位逐次减少1,末位都是8,中间的数位是随着小数部分位数的增加用9补充,增加一个数位就添一个9,增加两个数位就添两个9,依次类推,所以下面的被除数应该分别是5.59998和6.499998。再看商的变化规律,商都是小于1的小数,而且被除数有几位小数,商就有几位小数,商的十分位从3开始逐次增加1,十分位后面的数位上的数字都是2,所以5.59998÷9的商应该是0.62222,6.499998÷9的商应该是0. 722222。
解答: 0.32 0.422 0.5222
5.59998 0.62222 6.499998 0.722222
(2)计算前三个算式的商:
21.78÷0.4=54.45
219.78÷0.4=549.45
2199.78÷0.4=5499.45
观察上面三个算式,除数都是0.4,被除数和商同时发生变化。先观察被除数的变化规律,小数部分都是78,整数部分的前两位都是21 ,后面每个算式被除数整数部分的末尾都比上一个算式多一个9。再观察商的变化规律,商都是两位小数,且小数部分都是45,商的整数部分的位数与被除数的位数相同,且前两位都是54,后面数位用9补充,9的个数与被除数中整数部分末尾的9的个数相同。根据此规律,下面两个算式应该是21999.78÷0.4=54999.45,219999.78÷0.4=549999.45。
解答: 54.45 549.45 5499.45
21999.78 54999.45
219999.78 549999.45
第5题
49.5 49.95 49.995 49.9995
49.99995 49.999995
第6题
第7题
分析:第二个算式与第一个算式相比,第一个因数的小数部分增加了一个5,第二个因数整数部分的末尾增加了一个0;积的整数部分增加了一个4 ,小数部分增加了一个5。第三个算式与第二个算式相比,第二个因数整数部分的末尾增加了一个0,积的整数部分增加了一个4,积的小数部分增加了一个5。根据前面所发现的规律,第三个算式的第一个因数应在小数部分增加一个5,就是5.555;第四个算式的结果应该是44444.55555;第五个算式的结果应该是444444.555555。
解答:5.555 44444.55555 444444.555555
第8题
分析:观察每一横排算式的被除数,100-1=99,101-2=99,102-3=99……右边的被除数都比左边的多99,整理每排右边的算式可得到100÷99=(99+1)÷99=99÷99+1÷99,101÷99=(99+2)÷99=99÷99+2÷99……依次类推,发现每排右边的算式整理后都是在其左边算式的基础上多加了一个99÷99,即1,所以每排右边算式的结果为其左边算式的结果加1。
解答:
1÷99=0.01 100÷99=1.01
2÷99=0.02 101÷99=1.02
3÷99=0.03 102÷99=1.03
4÷99=0.04 103÷99=1.04
5÷99=0.05 104÷99=1.05
6÷99=0.06 105÷99=1.06
7÷99=0.07 106÷99=1.07
8÷99=0.08 107÷99=1.08
9÷99=0.09 108÷99=1.09
第9题
分析:(1)计算前三个算式:
0.9×0.9+0.69=1.5
9.8×0.9+1.68=10.5
98.7×0.9+11.67=100.5
观察三个算式,从第二个算式开始,每个算式的第一个因数每次增加一个数字,增加的数字都比前一个数字少1,且它们都是一位小数。第二个因数都是0.9。再观察每个算式的加数, 分别是1.68→11.67→111.66,整数部分的末尾依次增加一个数位,且增加的数位上的数字都是1,小数部分的位数不变,十分位上的数字不变,但百分位上的数字依次减1。再观察得数,得数都是一位小数,小数部分不变,整数部分的末尾依次增加一个0。根据此规律可知第四个算式的结果是1000.5,下面的算式可以是9876.5×0.9+1111.65=10000.5和98765.4×0.9+11111.64=100000.5,后两个算式答案不唯一。
(2)计算前三个算式:
0.1×0.9-0.01=0.08
1.2×0.9-0.01=1.07
12.3×0.9-0.01=11.06
观察三个算式,从第二个算式开始,每个算式的第一个因数每次增加一个数字,增加的数字都比前一个数字多1,且都是一位小数;第二个因数都是0.9;每个算式中的减数都是0.01;积分别是0.08→1.07→11.06,整数部分的末尾每次增加一个1,小数部分都是两位小数,每次减少0.01。根据此规律,下面的算式可以是123.4×0.9-0.01=111.05,1234.5×0.9-0.01=1111.04,12345.6×0.9-0.01=11111.03,答案不唯一。
解答:(1)1.5 10.5 100.5 1000.5
9876.5 1111.65 10000.5
98765.4 11111.64 100000.5(后两个算式答案不唯一)
(2)0.08 1.07 11.06
123.4 0.01 111.05
1234.5 0.01 1111.04
12345.6 0.01 11111.03(后三个算式答案不唯一)
6.解决问题
第1题
(1)C (2)B (3)B
第2题
(1)6 (2)7
第3题
分析:要将21 kg油分装在最多可以装2.5 kg的油桶里,求至少需要多少个这样的油桶,就是求21里面有几个2.5,用除法计算,即21÷2.5=8.4(个)。油桶个数应取整数,如果此题按照“四舍”法取近似数,就需要8个油桶,此时会剩下一些油,不符合题目要求,所以在此题中要按照“五入”法取近似数,即需要9个油桶。
解答:21÷2.5≈9(个)……5分
答:至少需要9个这样的油桶。……1分
第4题
(1)500÷40≈12(杯)
(2)5.5×12=66(g)
(3)66÷40≈2(盒)
第5题
50÷1.8≈27(个)
第6题
1.8÷24×10000=750(万件)
第7题
2.4×8.5×(20000÷100)=4080(kg)
第8题
分析:解答此题的关键是要知道倒出一半后连桶重的28 kg是剩下的一半油和一个桶的质量和,而最初的53 kg是一桶油和一个桶的质量和,从53 kg里减去28 kg,剩下的就是一半油的质量。用一半油的质量乘2就是一桶油的质量,再根据“单价×数量=总价”可计算出这桶油一共可以卖多少钱。
解答:(53-28)×2=50(kg)……4分
10.5×50=525(元)……4分
答:这桶油一共可以卖525元。……1分
第9题
33.7÷5.5≈7(个)
第10题
300000000÷10000×3.7×0.5=55500(吨)
第11题
分析:此题含有两个未知量,可以列出几组类似的数量关系式,观察数量关系式中的数据特点,然后设法消去一个未知量,只保留其中一个未知量,使数量关系式化繁为简。根据题意列数量关系式如下:
6个本+4支铅笔=4.6元……(1)
3个本+1支铅笔=1.9元……(2)
数量关系式中没有相同的量,可以把(1)式除以2 变成3个本+2支铅笔=2.3元……(3)
由(3)式-(2)式可以求出1支铅笔=(2.3-1.9)元,即1支铅笔的价钱是0.4元,根据1支铅笔的价钱和已知条件就可以求出1个本的价钱,即(1.9-0.4)÷3=0.5(元)或(4.6-4×0.4)÷6=0.5(元)。
解答:4.6÷2-1.9=0.4(元)……6分
(1.9-0.4)÷3=0.5(元)或(4.6-4×0.4)÷6=0.5(元)……6分
答:1个本的价钱是0.5元,1支铅笔的价钱是0.4元。……1分
