五年级数学（上册） - 五 简易方程
1.用字母表示数（1）用含有字母的式子表示简单的数量、数量关系和计算公式
第1题
（1）a－0.45 （2）s＋76 （3）3b
第2题
3b 6ac 5n 4a2 6.5t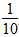 
m
第3题
（1）a－c （2）4b
第4题
24＋a 54元
第5题
（1）35 x （2）a b
第6题
（1）S＝ab C＝2（a＋b）
（2）S＝ab＝12×5＝60（cm2）
C＝2（a＋b）＝2×（12＋5）＝34（cm）
第7题
s÷6 500÷v 90t
第8题
分析：小正方形的边长是m cm，则小正方形的周长就是4m cm，即大正方形的边长是4m cm，再用4m cm乘4就是大正方形的周长,即4m×4＝16m（cm）。
解答: 4m×4＝16m（cm） ……7分
答：大正方形的周长是16m cm。……1分
1.用字母表示数(2)用含有字母的式子表示稍复杂的数量、数量关系和计算公式
第1题
15 8＋7n
第2题
（1）a＋b （2）282头
第3题
（1）180＋12a
（2）180＋12a＝180＋12×20＝420
第4题
分析：已知粮店运进大米a袋，每袋30 kg;面粉b袋，每袋20 kg。30a就是30×a，表示a袋大米共重多少千克；20 b就是20×b，表示b袋面粉共重多少千克；30a+20b表示a袋大米和b袋面粉共重多少千克。
解答：运进大米的总千克数
运进面粉的总千克数
运进大米和面粉的总千克数
第5题
300－3a 60元
【※浙江专用】5.100-3a 10元
第6题
分析：根据正方形的面积公式可求出空白部分的面积是a×a ＝ a 2（cm2）。阴影部分的面积＝大长方形的面积-正方形的面积，大长方形的长是b cm，宽是a cm，则大长方形的面积是a×b＝ ab（cm2），所以阴影部分的面积＝ab-a2（cm2）。
解答：空白部分：a 2 阴影部分：ab- a 2
1.用字母表示数(3)化简含有字母的式子
第1题
8a 2n 29a 27y
第2题
（1）8a＋8b （2）a＋1 （3）6a
第3题
（1）×（2）×（3）√（4）×
第4题
（1）xt＋yt （2）1035 km
【※浙江专用】4. （1）xt+yt （2）36 km
第5题
（1）90a分钟 4a万千米
（2）24×60÷90＝16（圈）
16×4＝64（万千米）
第6题
分析：（1）观图，1张餐桌，上、下方各坐1人，两边各坐1人，一共可坐4人； 2张餐桌，两边坐的人数不变，上、下方各多坐1人，一共可坐2×2+2＝6（人）； 3张餐桌，两边坐的人数不变，上、下方比2张餐桌各多坐1人，一共可坐2×3+2＝8（人）；同理， 4张餐桌可坐2×4+2＝10（人）； 5张餐桌可坐2×5+2＝12（人）； n张餐桌可坐（2n+2）人。
解答：
（1）
……6分
（2）2n+2＝2×12+2＝26……3分
答：拼12张餐桌可以就餐26人。……1分
2.解简易方程(1)方程的意义
第1题
①④⑥ ②③⑤
第2题
（1）X （2）X （3）√
（4）X （5）X （6）X
第4题
3x＝15
第5题
（1）2x＋58＝96
（2）3x＋42.6＝81
第6题
分析：用两根一样长的细铁丝折成的长方形和正方形的周长是相等的，根据这个等量关系可以列出方程。
解答：4a＝（12＋8）×2
2.解简易方程(2)等式的性质
第1题
（1）8 （2）36
第2题
（1）3 平衡 （2）1 平衡 5
第3题
分析：（1）从图中可知，把一个球和一个小正方体放在天平的两边，天平保持平衡；把左边球的数量扩大到原来的4倍就是4个，那么右边小正方体的数量也应扩大到原来的4倍，才能使天平保持平衡。
（2）从图中可知，天平左边的梨由2个变成1个，天平右边的桃子由4个变成2个，说明把天平两边的水果都平均分成2份，各去掉1份，天平仍保持平衡，说明1个梨和2个桃子同样重。
解答：（1）4 平衡 （2）2 平衡 2
第4题
2
第5题
分析：从前两架天平的情况可列出如下关系式：
1个橘子+2个桃子＝2个苹果
3个苹果＝3个橘子+2个桃子
第三架天平右边的托盘中有4个橘子和4个桃子，正好是把第一架天平左边托盘中的水果和第二架天平右边托盘中的水果合并到一起，对应的另外两个托盘中一共是5个苹果，所以只要在第三架天平左边的托盘中放5个苹果，就能使天平保持平衡。
解答:5个
第6题
分析：观察下面4个算式：
A+B+C＝61
A+C+D＝71
A+B+D＝62
B+C+D＝64
不难发现，四个算式的等号左边一共有3个A，3个B，3个C和3个D，把四个算式的等号左边和等号右边分别加在一起变成3（A+B+C+D）＝61+71+62+64，通过整理得到A+B+C+D＝86。
解答：（61＋71＋62＋64）÷3＝86
3.解方程(1)简易方程
第1题
（1）－ 3 （2）＋ 10
第2题
（1）X（2）√（3）X
第3题
第4题
x＝91.4 x＝28.8
第5题
（1）÷ 3 （2）4x＝32 8
第6题
（1）4x＝6 x＝1.5
（2）1.2x＝30 x＝25
（3）x＋5.2＝7.8 x＝2.6
第7题
（1）x＝11 （2）x＝10 （3）x＝3
（4）x＝100
第8题
分析：要使每个方程的解都是8，只要把8当成已知数代入方程即可求出（ ）里应填的数。（ ）+x＝8.4，可以转化成（ ）+8＝8.4，等式两边同时减去8，（ ）里应填0.4；x -（ ）＝7.2，可以转化成8-（ ）＝7.2，根据“减数＝被减数－差”可知（ ）里应填0.8；x×（ ）＝12，可以转化成8×（ ）＝12，等式两边同时除以8，（ ）里应填1.5；x÷（ ）＝20, 可以转化成8÷（ ）＝20，根据“除数＝被除数÷商”可知（ ）里应填0.4。
解答：0.4 0.8 1.5 0.4
3.解方程(2)稍复杂的方程
第1题
第2题
（1）－ 1.5 － 1.5 4.5
÷ 3 4.5 ÷ 3 1.5
（2）＋ 8 ＋ 8 18.6
÷ 6 18.6 ÷ 6 3.1
第3题
（1）3x＋12＝75 （2）3x－15＝60
第4题
x＝8.8 x＝6.2 x＝36.8 x＝10
第5题
（1）B （2）C （3）A
第6题
x＝8 x＝2.5
第7题
分析：计算本题中的两个小题时，先求出已知方程的解，再把这个解代入后面的算式中即可求出（ ）里应填的数。
解答：（1）6.32 （2）26.5
4.实际问题与方程(1)实际问题与方程(一)
第1题
（1）5.6＋x＝12.5 （2）3x＝37.5
（3）4x＋35＝115 （4）x＋5x＋12＝480
第2题
（1）运来的50箱 － 卖出的箱数
（2）路的全长 －
（3）× 宽 （4）－ ＋
第3题
分析：（1）平均分给x个班，每班分6个，求一共有多少个乒乓球，就是求x个6是多少，列方程为6 x ＝72；72个乒乓球，平均分给x个班，求每班分几个，列方程为72÷x＝6。
（2）算式结果是5 ，根据已知条件可知求的是爸爸今年的年龄比欢欢的4倍多多少岁，爸爸今年37岁，欢欢今年x岁，欢欢年龄的4倍就是4x，可列方程37-4x ＝5；算式结果是37，就是求爸爸的年龄，因为爸爸今年的年龄比欢欢的4倍还多5岁，所以可列方程4x +5＝37。
解答：（1）6x 72÷x
（2）37－4x 4x＋5
第4题
解：设长江长约x km。
x＋370＝6670
x＝6300
第5题
解：设梵蒂冈的面积约是x km2。
6x＋0.26＝2.9
x＝0.44
【※浙江专用】
5.解：设云台山玉女峰海拔x m。
3x +54＝1929
x＝625
第6题
解：设我国烟民数量约是x亿人。
3x－1.6＝7.4
x＝3
第7题
解：设水星绕太阳一周大约要用x天。
4x＋13＝365
x＝88
第9题
解：设小男孩收集了x枚奥运邮票。
2x－15＝185
x＝100
第10题
分析：（1）此题可以用算术方法解答，也可以列方程解答。
算术方法：甲桶油比乙桶油多，可以把甲桶油看成是两部分，一部分是和乙桶油同样多的部分，另一部分是比乙桶油多的部分，甲桶油比乙桶油多50-36＝14（kg），把多的14 kg平均分成2份，把其中的1份倒给乙桶，就能保证两桶油的质量相等。
列方程解答：首先要找到等量关系，甲桶倒出部分油给乙桶后两桶油的质量相等。可以设从甲桶中倒出x kg油到乙桶，两桶油的质量相等。等量关系式是甲桶油的质量- x ＝乙桶油的质量+ x。
（2）此题列方程解答比较简便。
根据题意列出等量关系式：（甲桶油的质量-甲桶倒出油的质量）×1.5＝乙桶油的质量+甲桶倒出油的质量，然后根据这个等量关系式列方程。
解答：（1）算术方法：（50-36）÷2＝7（kg）……9分
列方程：解：设从甲桶中倒出x kg油到乙桶，两桶油的质量相等。……1分
50-x＝36+x……5分
x＝7……2分
答：从甲桶中倒出7 kg油到乙桶，两桶油的质量相等。……1分
（2）解：设从甲桶中倒出x kg油到乙桶，乙桶油的质量是甲桶油的1.5倍。……1分
（50-x）×1.5＝36+x……5分
x＝15.6……2分
答：从甲桶中倒出15.6 kg油到乙桶，乙桶油的质量是甲桶油的1.5倍。……1分
4.实际问题与方程(2)实际问题与方程(二)
第1题
第2题
（1）x＋3x＝180 x＝45
（2）42.5＋3x＝143 x＝33.5
（3）3x－x＝32 x＝16
第4题
（1）分析：商店运来的苹果总质量减去卖出的苹果质量就是剩下的苹果质量，商店运来的苹果总质量根据运来8箱苹果，每箱x kg可以求出。
解答：关系式：苹果总质量-卖出的苹果质量＝剩下的苹果质量
方程：8x-44＝116
（2）分析：商店运来的苹果总质量减去剩下的苹果质量就是卖出的苹果质量。
解答：关系式：苹果总质量-剩下的苹果质量＝卖出的苹果质量
方程：8x-116＝44
（3）分析：题中有三个量，苹果总质量，卖出的苹果质量和剩下的苹果质量，前两个题等号右边分别是剩下的苹果质量和卖出的苹果质量，这个题可以把苹果总质量放在等号右边，即卖出的苹果质量加上剩下的苹果质量就是苹果的总质量。
解答：关系式：卖出的苹果质量+剩下的苹果质量＝苹果的总质量
方程：44+116＝8x
第5题
解：设每平方米的夹竹桃叶能吸附灰尘x g，则每平方米的榆树叶能吸附灰尘1.6x g。
x＋1.6x＝20.8 x＝8
8×1.6＝12.8（g）
第6题
解：设颐和园的陆地面积大约有x公顷，则颐和园的水面面积大约有3x公顷。
3x＋x＝290 x＝72.5
72.5×3＝217.5(公顷)
第7题
解：设小明今年x岁，则妈妈今年5x岁。
5x－x＝28 x＝7
7×5＝35（岁）
第9题
分析：利用方程解答此题。设这条鱼的尾长为x dm。根据已知条件可知：身长＝头长+尾长……（1），尾长＝头长+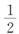 
身长……（2）。
把（1）式代入（2）式可得到：尾长＝头长+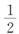（头长+尾长），把已知数据代入关系式即可求出尾长。
解答：解：设这条鱼的尾长为x dm。……1分
3+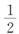×（3+ x）＝x……7分
x＝9………2分
答：这条鱼的尾长为9 dm。……1分
第10题
分析：设一共取了x次。因为每次取走8个乒乓球，x次正好取完，所以共有8x个乒乓球；因为每次取走6个羽毛球，取x次后还剩10个，所以一共有（6x+10）个羽毛球，根据题中的等量关系“乒乓球的数量＝羽毛球的数量”，可列出方程8x＝6x+10，最后根据求出的次数求出每种球的数量。
解答：解：设一共取了x次。……1分
8x＝6x+10……6分
x＝5……2分
5×8＝40（个）……2分
答：一共取了5次，原来两种球各有40个。……1分
4.实际问题与方程(3)解决问题
第1题
（1）小红走的路程 小华走的路程 总路程
0.28x＋0.27x＝5.5
（2）小汽车行的路程 货车行的路程
总路程
65×2.5＋2.5x＝282.5
（3）小亮走的路程 小刚走的路程 小亮比小刚多走的路程
6x－68×6＝72
第2题
（1）甲车 乙车 936
（2）解：设乙车平均每小时行x km。
95×5.2＋5.2x＝936
x＝85
第3题
分析：先根据题意列出等量关系式：李老师所走的路程-小刚所走的路程＝66 m，然后根据这个等量关系式列出方程并求解。
解答：解：设x分钟后,小刚落后李老师66 m。……1分
82x-60x＝66……4分
x＝3……2分
答：3分钟后,小刚落后李老师66 m。……1分
第4题
分析：先根据题意列出等量关系式：师傅9小时的工作量+徒弟9小时的工作量+70个＝ 520个,然后根据这个等量关系式列方程并求解。
解答：解：设徒弟平均每小时加工x个。……1分
30×9+9x+70＝520……4分
x＝20……2分
答：徒弟平均每小时加工20个。……1分
第5题
分析：本题属于相遇问题，根据题意可列出等量关系式：小明5分钟走的路程+小明10分钟走的路程+小刚10分钟走的路程＝总路程，进而得出“小明的速度×5+小明的速度×10+小刚的速度×10＝总路程”。小刚骑车比小明步行每分钟多行130 m，把小明步行的速度设为x米/分，则小刚骑车的速度为（130+x）米/分，然后列出方程并求解。
解答：解:设小明步行每分钟行x m。……1分
5x+10x+10×（130+x）＝2800……5分
x＝60……3分
答：小明步行每分钟行60 m。……1分