五年级数学(上册) - 六 多边形的面积
1.平行四边形的面积
第2题
(1)正方形 长方形 (2)无数 (3)ah (4)相等
第3题
分析:(1)此题错误。一个平行四边形通过分割平移转化为一个长方形时,无论怎样分割、平移、转化、拼接, 始终都是把直角三角形或直角梯形的斜边拼接,直角三角形或直角梯形的直角边变成了长方形的宽,因为斜边大于直角边,所以转化后的周长缩短了,但面积不变,如图。
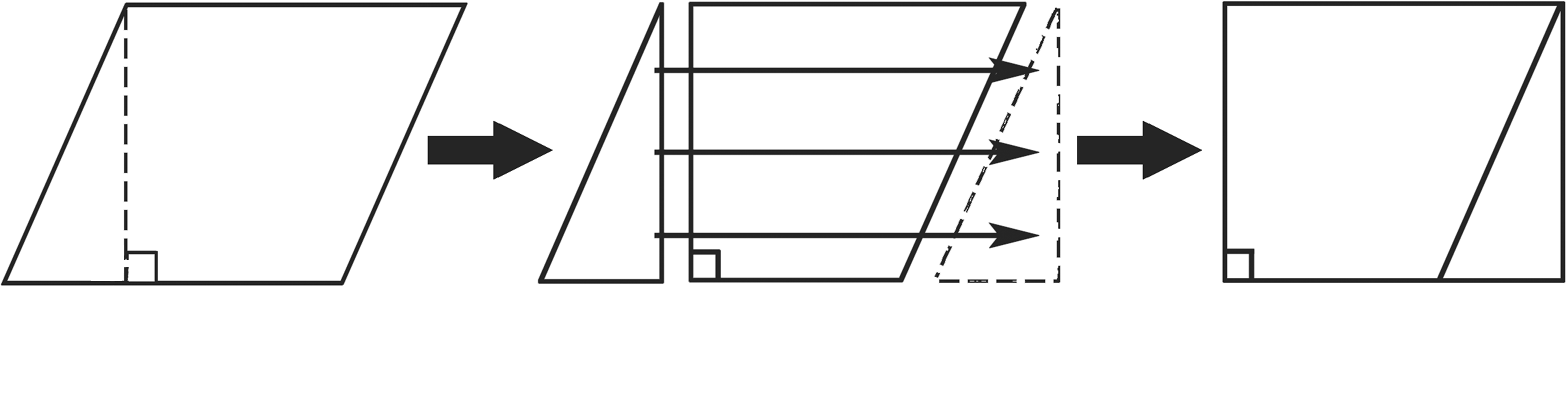

(2)此题正确。把一个长方形木框拉成一个平行四边形 ,木框长短没有变化,所以周长不变,但是木框被拉扁了,也就是高变短了,长没变,所以面积变小了。
(3)此题错误。因为平行四边形的面积不只与高有关,还与底有关。
(4)此题错误。平行四边形面积的大小与形状无关,与底和高有关,只要平行四边形底和高的乘积相等,不管什么形状的平行四边形面积都相等。
(5)此题错误。平行四边形的面积=底×高,(底×3)×(高×3)=底×高×9,即面积扩大到原来的9倍。
解答:(1)× (2)√ (3)× (4)× (5)×
第4题
(1)10×8=80(cm2)
(2) 分析:观察图中的两个平行四边形,它们有一个共同的底,且高相等,所以它们的面积一定相等。
解答:两个平行四边形的面积相等。……3分
1.8×1.2=2.16(cm2)……3分
第5题
345÷20=17.25(dm)
第6题
8×8÷5=12.8(cm)
第7题
98.6÷11.6=8.5(dm)
第8题
(1)40×10×20=8000(棵)
(2)800÷(40×10)=2(棵)
第9题
分析:观察图形,阴影部分的面积=平行四边形的面积-①的面积。①的面积已知,只要求出平行四边形的面积即可。因为平行四边形的底是长方形的长,平行四边形的高是长方形的宽,所以平行四边形的面积就等于长方形的面积。
解答: 16×10-50……5分
=110(cm2)……3分
第10题
分析:由题可知,种草部分的面积=平行四边形的面积-小路的面积。把小路右面的草坪向左平移1米,即可变成一个长是4.5-1=3.5米,高是3米的平行四边形草坪,利用平行四边形的面积计算公式可以求出草坪的面积,也就是种草部分的面积。
解答: (4.5-1)×3……6分
=10.5(m2)……4分
答:种草部分的面积是10.5㎡。……1分
2.三角形的面积
第1题
(1)A C B D
(2)2 高 底 底×高÷2 S=ah÷2
第2题
分析:(1)此题错误。只有等底等高的平行四边形的面积才是三角形面积的2倍。
(2)此题错误。两个等底等高的三角形的形状不一定完全相同,所以等底等高的两个三角形不一定能拼成一个平行四边形。
(3)此题错误。三角形的高扩大到原来的4倍,底不变,面积扩大到原来的4倍。
(4)此题错误。此题没有限定平行四边形和三角形的底和高的大小,所以不能确定谁的面积大,谁的面积小。
解答:(1)× (2)× (3)× (4)×
第3题
(1)A (2)B (3)B
第4题
(1)S=ah÷2=2.5×1.6÷2=2(dm2)
(2)S=ah÷2=3.7×2.4÷2=4.44(cm2)
第5题
24×15÷2×4=720(棵)
第6题
(1)ah÷2 (2)ah÷2 (3)ah÷2 相等
第7题
分析:从图中可以看出原三角形玻璃是个直角三角形,且是个等腰直角三角形,所以它的另一条直角边的长度也是8 cm,两条直角边的乘积除以2就是原三角形玻璃的面积。
解答:8×8÷2=32(cm2)……4分
答:原三角形玻璃的面积是32 cm2。……1分
第8题
40×2÷10=8(m)
8×2.5÷2×180=1800(元)
第9题
30×40÷2×2÷50=24(cm)
第10题
(1)
(2)168×2÷24×8÷2+168=224(m2)
第11题
方法一:剔除法。
分析:先求出两个正方形的面积和,再从中减去空白部分的两个三角形的面积,即为阴影部分的面积。
解答:5×5+3×3=34(cm2)……4分
3×(3+5)÷2+5×5÷2=24.5(cm2) ……4分
34-24.5=9.5(cm2) ……4分
方法二:分割法。
分析:将阴影部分分割成两个已知底和高的三角形,如下图,先分别求出两个阴影三角形的面积,再求整个阴影部分的面积。
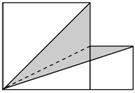
解答:3×3÷2+(5-3)×5÷2=9.5(cm2) ……12分
3.梯形的面积
第1题
A C 上底+下底 高 一半 (上底+下底)×高÷2 S=(a+b)h÷2
第2题
(1)× (2)× (3)× (4)√
第3题
(1)C (2)C (3)C B (4)D
第4题
(3.1+5.4)×1.6÷2=6.8(cm2)
第5题
(1)(4+8)×20÷2×2=240(cm2)
(2)(24+60)×30÷2÷0.8=1575(棵)
第6题
(64-19)×14÷2=315(m2)
第7题
(1)(42+76)×53÷2=3127(m2)
第8题
90×2÷(6+12)=10(m)
第9题
分析:由题意可知,如果直角梯形的下底减少15 dm,就变成了正方形,正方形的四条边相等,由此可知直角梯形的下底比上底多15 dm,梯形的高也和上底一样长。按照梯形的面积计算公式即可求出这个直角梯形的面积。
解答:25+15=40(dm)……4分
(25+40)×25÷2……4分
=812.5(dm2)……1分
第10题
分析:由题意可知,题中的两个直角三角形的面积相同,则梯形EFCG的面积+三角形CGD的面积与三角形CGD的面积+梯形ABGD的面积(阴影部分的面积)相等,由此可以得出,梯形EFCG的面积和梯形ABGD的面积相等。求出梯形EFCG的面积就可以求出阴影部分的面积。
解答:(5+7)×6÷2……7分
=36(cm2) ……5分
4.组合图形的面积(1)组合图形的面积
第2题
第3题
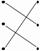
分析:(1)由图可知,三个图形的高是一样的,平行四边形的面积是4h,三角形的面积是8h÷2=4h,梯形的面积是(2+6)h÷2=4h,所以三个图形的面积一样大。
(2)由题意可知,三个长方形是完全相同的,甲的面积正好是长方形的一半;乙的底是长方形的长,它的高是长方形的宽,它的面积就是长方形的一半;丙的底是长方形的宽,高是长方形的长,它的面积也是长方形的一半,所以这三个图形的面积一样大。
解答:(1)D (2)D
第4题
10×10+10×4÷2=120(m2)
第5题
分析:(1)用分割法求:先将图形分割成三部分,即两个同样大的梯形和一个长方形,然后分别求出两个梯形的面积和长方形的面积,最后把三个图形的面积相加。
解答:(6-1.5)÷2=2.25(cm)……1分
(2+2.25)×2÷2×2=8.5(cm2)……2分
6×(4-2)=12(cm2)……2分
8.5+12=20.5(cm2)……1分
(2)用添补法求:先连线,使原图形成为一个完整的长方形,连线后的图形中间的部分是个梯形,然后分别求出长方形的面积和梯形的面积,最后再相减,即可求出图形的面积。
解答:6-2-2=2(cm)……3分
6×4-(1.5+2)×2÷2=20.5(cm2)……3分
第6题
(1) 分析:辅助线把原图形分成一个梯形和一个长方形,先分别求出梯形的面积和长方形的面积,再相加,即可求出原图形的面积。
解答:(3+4)×(4-2)÷2+4×2=15(dm2)
(2) 分析:辅助线把原图形分成一个梯形和一个长方形,先分别求出梯形的面积和长方形的面积,再相加,即可求出原图形的面积。
解答: (2+4)×(4-3)÷2+3×4=15(dm2)
(3) 分析:辅助线把正方形缺的部分补上了,只要先分别求出原正方形的面积和三角形的面积,再相减,即可求出图形的面积。
解答:4×4-(4-3)×(4-2)÷2=15(dm2)
第7题
6×6+4×4-(6+4)×6÷2=22(cm2)
第8题
分析:此题可用剔除法解决。长方形中“Y”以外有三部分,分别是一个三角形和两个梯形。从长方形的面积中剔除一个三角形的面积和两个梯形的面积,即是“Y”的面积。
解答:6×8-3×(8-4)÷2-(4+8)×2÷2×2……5分
=48-6-24……2分
=18(cm2)……2分
第9题
分析:在图中作两条辅助线把阴影部分分成三部分:两个同样的长方形和一个正方形,如图所示:
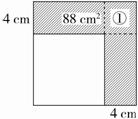
用阴影部分的面积减去①的面积,所得的差再除以2就是其中一个长方形的面积,长方形的面积再除以它的宽4 cm,可得到长方形的长,即原正方形的边长。
解答:(88-4×4)÷2÷4……6分
=9(cm)……2分
9×9=81(cm2)……3分
4.组合图形的面积(2)解决问题
第4题
15×10=150(m2)
第5题
(25+35)×10÷2=300(m2)
300×4=1200(棵)
第6题
分析:草坪的形状可以近似地看成一个长方形,通过数一数可以发现,长方形的长约是9个格,宽约是6个格,求出长方形的面积后再减去中间的正方形的面积就是草坪的面积。
解答:9×6-3×3=45(m2)……12分
答:这块草坪的面积大约是45 m2。……1分
