五年级数学(上册) - 专项全练全测答案
学习领域专项全练全测(一)
第一题
1.140 4 2.0.627 62.7 0.0627
3.6.996 7 7.00 4.8a+b 94
5.3.1
6.< > = < < =
7.21 0.4
8. 分析:把a的小数点向右移动一位就是扩大到原来的10倍,这时和b相等,即b=10a,根据已知条件可列出等式a+10a=1.65,求得a=0.15,代入b=10a,求得b=1.5。
解答:0.15 1.5
第二题
分析:1.此题错误。积的小数位数应与几个因数中的小数位数和相同,当两个因数相乘积的末位有0时,根据小数的基本性质可以去掉0,简写后积的小数位数少于两个因数中的小数位数和。
2.此题错误。0.56666虽然有4个相同的数字重复,但它是有限小数。
3.此题正确。除数是0.01,在计算时要把0.01扩大到原来的100倍,变成整数后计算,为了使商不变,被除数也要扩大到原来的100倍,所以一个数(0除外)除以0.01等于把这个数扩大到原来的100倍。
4.此题错误。在除法算式中,商随着被除数的扩大而扩大,商随着除数的扩大而缩小。在此题中,被除数扩大到原来的100倍,商也扩大到原来的100倍变成300,除数扩大到原来的10倍,那么商就缩小到原来的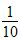 ,商变成30。
,商变成30。
5.此题正确。根据“四舍五入”法求近似数时,计算时要比保留的位数多算一位。精确到百分位,就是保留两位小数,所以要除到小数点后的第三位。
解答:1.× 2.× 3.√ 4.× 5.√
第三题
1.C 2.C 3.B 4.C 5.A
第四题
1.0.1 2.6 9.8 0.1 21 0.248 100
1 50 7 520 0.03
2.8.512 20
3.0.84×1.2+8.4×0.88
分析:在两个乘法算式中两个因数0.84和8.4中都含有数字8、4,只是两个小数的大小不同,可以在积不变的前提下,通过移动小数点的位置将这两个小数转化成相同的小数,即先把0.84×1.2变成8.4×0.12,再用乘法分配律进行计算。
解答: 0.84×1.2+8.4×0.88
=8.4×0.12+8.4×0.88……1分
=8.4×(0.12+0.88)……1分
=8.4……1分
0.25×32×1.25
分析:先把32写成4×8的形式,再用乘法结合律进行简算。
解答: 0.25×32×1.25
=0.25×4×8×1.25……1分
=(0.25×4)×(8×1.25)……1分
=10……1分
4.8÷0.16÷3
分析:利用除法的运算性质a÷b÷c=a÷(b×c)(b,c不等于0)进行简算。
解答: 4.8÷0.16÷3
=4.8÷(0.16×3)……1分
=4.8÷0.48……1分
=10……1分
4. x=1.4 x=2.2 x=3.45
第五题
分析:从上往下观察第一个因数的变化规律,各个数位上都是5,整数部分不变,每次变化都是在小数部分的末尾增加一个5;再看第二个因数,小数部分不变,始终是1,每次变化都是在整数部分的末尾增加一个0;最后观察积的变化规律,整数部分由4组成,小数部分由5组成,前面的因数中共含有几位小数,积中的4和5的个数就有几个。
解答:44444.55555
444444.555555
4444444.5555555
第六题
1.解:设天安门广场的面积约是x万平方米。
2x-16=72
x=44
【※浙江专用】675÷4.5=150(km)
(1650-675)÷150=6.5(小时)
2.150÷13.8≈10(个)
150÷(13.8-1.8)≈12(个)
12-10=2(个)
3.170.3÷2.6=65.5(千米/时)
255.5÷3.5=73(千米/时)
73>65.5 轿车的速度快。
4.分析:从第1根电线杆到第21根电线杆,共有20个间隔,小军用了5分钟,由此可以计算出他一分钟经过(21-1)÷5=4(个)间隔,从而可计算出他30分钟经过4×30=120(个)间隔,最后加1就是所求电线杆的数量。
解答:(21-1)÷5=4(个)……2分
4×30+1=121(根)……2分
答: 他应该骑到第121根电线杆。……1分
5.分析:根据题意可知,乙队比甲队多挖了256 m,从总长中减去256 m得到的就是两个甲队所挖的米数,除以2就是一个甲队所挖的米数,从而可以求出甲队平均每天挖的米数。乙队32天比甲队多挖了256 m,可求出乙队一天多挖的米数,从而可以求出乙队每天挖的米数。
解答:(2816-256)÷2÷32=40(m)
40+256÷32=48(m)
答:乙队平均每天挖隧道48 m。
学习领域专项全练全测(二)
第一题
1. 15.6
2. (4,5)
3.列
4. 6
5. 分析:S=ah,(a×3)×(h×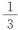 )=ah,因此,面积不变。
)=ah,因此,面积不变。
解答:300
6.10
7.30
8.10
9.12.5 cm2
第二题
1.分析:必须是两个完全一样的三角形才能拼成一个平行四边形。
解答:×
2.分析:三角形的面积=底×高÷2,底×(高×4)÷2=底×高×2,面积扩大到原来的4倍。
解答:×
3.分析:平行四边形的面积既与高的长度有关,还与底的长度有关,如一个平行四边形的高是4,底是5,另一个平行四边形的高是10,底是2,这两个图形的面积相等,高却不相等。
解答:×
4.分析:平行四边形和长方形的面积大小与周长没有直接关系。如平行四边形的高是4,底是5,长方形的长是10,宽是2,这两个图形的周长不相等,面积却相等。
解答:×
5.分析:任意一个梯形沿对角线剪开都是两个等高的三角形。
解答:√
第三题
1.分析:图中的平行四边形和三角形等底等高,平行四边形的面积是三角形的2倍;图中的梯形与平行四边形、三角形等高,梯形的下底是4,上底比4小,上底和下底之和除以2比4小,所以它的面积也比平行四边形的面积小。
解答:A
2.分析:把长方形木框拉成平行四边形后,各条边的长短不变,即周长不变;但可以看到木框的形状变扁了,也就是它的高变短了,自然面积就变小了。
解答:C A
3.分析:三个图形中的三个三角形的底都是完全一样的平行四边形的底,它们的高也都是平行四边形的高,所以它们的面积也是相等的。
解答:A
4.分析:梯形面积=(上底+下底)×高÷2,变化后,梯形的面积是(上底×2+下底×2)×高÷2= (上底+下底)×2×高÷2,即面积是原来的2倍。
解答:A
5.C
第四题
1.2 2 (2,2) (4,1)
2.西红柿 茄子 辣椒
第六题
方法一:分析:可以把原图形分成一个长方形和一个梯形,如下图所示:
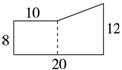
解答:10×8+(8+12)×(20-10)÷2=180 (cm2)
方法二:分析:可以把原图形分成一个长方形和一个三角形。如下图所示:
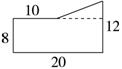
解答:8×20+(20-10)×(12-8)÷2=180(cm2)
【※浙江专用】略
第七题
1.(30-12)×12÷2=108(m2)
2.(36-2)×23=782(m2)
3.分析:需要粉刷的面积=三角形的面积+长方形的面积-窗户的面积,用需要粉刷的面积乘每平方米的涂料质量就得出涂料的总质量,再用涂料的总质量乘2.5就得出买涂料需要的总钱数。
解答:(1)6.2×1.6÷2=4.96(m2)……2分
6.2×3-1.2×1.5=16.8(m2)……2分
4.96+16.8=21.76(m2)……1分
答:需要粉刷的面积是21.76 m2。……1分
(2)21.76×0.56×2.5≈31(元)……5分
答:李大伯粉刷这面墙要用31元钱。……1分
4.分析:阴影部分的面积可由两个正方形的面积和去除空白面积求出。
解答:6×6+8×8=100(cm2)……2分
6×6÷2=18(cm2)……2分
(8-6)×8÷2=8(cm2)……1分
8×(8+6)÷2=56(cm2)……1分
100-18-8-56=18(cm2)……1分
学习领域专项全练全测(三)
第一题
1. 分析:(1)指针一定停在红色区域,则必须所有区域都是红色。②号转盘符合条件。
(2)指针不可能停在绿色区域,则所有的区域都不是绿色。②号转盘符合条件。
(3)指针可能停在蓝色区域,说明这个蓝色区域必须存在,不论多少。①号转盘符合条件。
解答:(1)② (2)② (3)①
2.黄
3. 分析:盒子里有红色和黄色两种球,所以任意摸一个可能是红色的,也可能是黄色的。哪种球的个数多,摸出的可能性就大,黄球多,摸出的次数可能就多;红球少,摸出的次数可能就少。
解答:(1)红 黄
(2)黄 红
(3)黄
4.一定 不可能
第三题
1.分析:平均水深是1.2 m,不是指所有水域都是1.2米深,最深处可能是2 m,还可能更深。
解答:×
2.分析:只要参加比赛,任何人都有得第一的可能性,明明也不例外。
解答:√
3.分析:硬币抛出后,正面朝上和反面朝上的可能性相等,理论上抛10次是正面朝上和反面朝上各5次,但抛硬币是随机事件,只能说抛的次数越多,正面朝上和反面朝上的次数越接近。
解答:×
4.分析:全校师生名单里也包括老师,所以任意指出一个,可能是学生,也可能是老师。
解答:×
5.分析:小娟学习刻苦,只能说她可能成为科学家。
解答:×
第四题
1.A
2. 分析:哪种颜色的份数多,指针指向哪个区域的可能性就大。
解答:B
3. 分析:盒子里有红色和绿色两种颜色的跳棋,并且红色占8个,绿色占2个,任意摸出两个,可能摸出的都是红色,也可能都是绿色,还可能是一个红色一个绿色。
解答:C
4.C
5. 分析:任意摸三块,可能都是水果糖,也可能都是巧克力糖,还可能是一块水果糖和两块巧克力糖或两块水果糖和一块巧克力糖。
解答:B
第六题
1.(1)菲菲 (2)宁宁 (3)宁宁 (4)明明
2.分析:不可能是黄球,那么盒子里就是没有黄球。第4个盒子符合条件;一定是黄球,那么盒子里就都是黄球,第一个盒子符合条件;可能是黄球,说明盒子里存在的不只是黄球,那么第2、3、5个盒子都符合条件;黄球的可能性很小,说明黄球在盒子里的个数比其他颜色的球少得多,第2个盒子符合条件;黄球的可能性很大,说明黄球在盒子里的个数比其他颜色的球多得多,第3个盒子符合条件。
解答: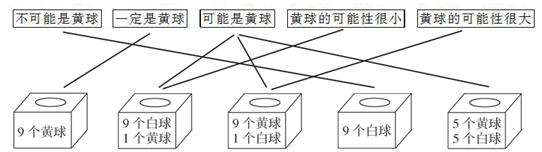
3.分析:卡片上有几个数字,任意摸出一张摸到的数字就有几种可能。哪个数字的卡片数量多,摸到的可能性就大,哪个数字的卡片数量少,摸到的可能性就小。
解答:4 9 1
4. 分析:一共20名同学,要想捉到女同学的可能性大,那么女同学的数量就要大于男同学的数量。所以至少要有11名女同学。
解答:女同学至少要有11名。
薄弱环节专项全练全测(一)
第二题
1.8.2 54 0.57 5.03 0.5 15
2.38.4 4.325
第三题
1.分析:此题错在把乘法结合律和乘法分配律弄混了。
解答:12.5×32
=12.5×(8×4)……1分
=12.5×8×4……1分
=100×4……1分
=400……1分
2.分析:0.47×9.9,把9.9改写成10-0.1,然后利用乘法分配律进行计算。
解答:0.47×9.9
=0.47×(10-0.1)……1分
=0.47×10-0.047……1分
=4.7-0.047
=4.653……1分
分析:7.8×11-7.8,减号后的7.8可以写成7.8×1,然后利用乘法分配律进行计算。
解答:7.8×11-7.8
=7.8×11-7.8×1……1分
=7.8×(11-1)……1分
=7.8×10
=78……1分
分析:35.79×99+35.79,加号后35.79可以写成35.79×1,然后利用乘法分配律进行计算。
解答:35.79×99+35.79
=35.79×99+35.79×1……1分
=35.79×(99+1)……1分
=35.79×100
=3579……1分
第四题
1.1020÷6.80=150(升) (6.80+0.60)×150=1110(元)
3.(1)(5-2)×1.5+6=10.5(元) (2)(15-6)÷1.5+2=8(km)
第五题
1.8+k
2.2m+n
3.x÷y
4.x+2y
第六题
1.A 2.C 3.B
第七题
1.分析:先根据题意找出题中的等量关系:五年级植树的棵数×4+16=456,然后根据等量关系式列方程解答。
解答:解:设五年级植树x棵。……1分
4x+16=456……2分
x=110……2分
答:五年级植树110棵。……1分
2.分析:先根据题意找出题中的等量关系:(甲船的速度+乙船的速度)×6=486,然后根据等量关系式列方程解答。
解答:解:设甲船每小时行驶x km。……1分
(x+45)×6=486……2分
x=36……2分
答:甲船每小时行驶36 km。……1分
第八题
分析:时钟敲8下应有7个间隔,14秒敲完,那么一个间隔的时间是(14÷7)秒。时钟敲12下是(12-1)个间隔,乘一个间隔的时间即可求出问题。
解答:14÷(8-1)=2(秒)……3分
2×(12-1)=22(秒)……4分
答:12时敲了12下,用了22秒。……1分
薄弱环节专项全练全测(二)
第一题
1. 2.5 2. 24
3. 分析:要求平行四边形的面积和梯形的面积需要知道底和高,底已知,它们的高和三角形的高相等,三角形的面积和底是已知的,高=面积×2÷底。
解答:40 52
4. 30 60
第二题
1.× 2.× 3.× 4.× 5.×
第三题
1.5×8÷2=20(cm2)
2.(4+7)×4÷2=22(cm2)
第四题
1.24×2÷5=9.6(cm)
2.100×2÷10=20(cm) 20-12=8(cm)
3.1.5×2÷2×2÷1.2=2.5(m)
第五题
1. 分析:阴影部分是个梯形,利用面积公式即可求出。
(1.6+4.8)×3.5÷2……3分
=11.2(cm2)……2分
【※浙江专用】(4+6)×4÷2=20(cm2)
2.分析:因为A、B两点是大平行四边形上下两边的中点,所以由虚线和上下两边组成的小平行四边形的面积就是大平行四边形的一半。阴影部分是和小平行四边形等底等高的三角形,面积正好是小平行四边形的一半。
解答:64÷2÷2……3分
=16(cm2)……2分
3.计算此图形有多种方法,列举三种如下:
方法一:分析:可以把原图形分成一个长方形和一个梯形,如下图所示:
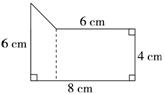
解答:列综合算式:
6×4+(4+6)×(8-6)÷2……4分
=34(cm2)……2分
分步计算:6×4=24(cm2)……2分
(4+6)×(8-6)÷2=10(cm2)……2分
24+10=34(cm2)……2分
方法二:分析:可以把原图形分成一个长方形和一个三角形。如下图所示:
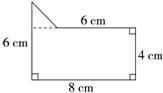
解答:列综合算式:
8×4+(8-6)×(6-4)÷2……4分
=34(cm2)……2分
分步计算:8×4=32(cm2)……2分
(8-6)×(6-4)÷2=2(cm2)……2分
32+2=34(cm2)……2分
方法三:分析:可以把原图形分成一个梯形和一个三角形。如下图所示:
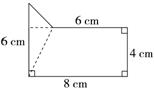
解答:列综合算式:
(6+8)×4÷2+6×(8-6)÷2……4分
=34(cm2)……2分
分步计算:(6+8)×4÷2=28(cm2)……2分
6×(8-6)÷2=6(cm2)……2分
28+6=34(cm2)……2分
第六题
1.5×7+7×1.6÷2-2×1.5=37.6(m2)
2. 分析:这堆钢管横截面是梯形,可以把最上面一层的钢管根数看作上底,最下面一层的钢管根数看作下底,层数看作高,求出面积即总根数。最上层有2根,最下层有12根,应该有(12-2+1)层。
解答:(2+12)×(12-2+1)÷2……6分
=77(根)……2分
答:这堆钢管共有77根。……1分
第七题
1.(3,8) (7,7) (2,3) (9,5)
