1.分数混合运算 - 精版答案
第1题
(1)乘 减 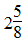
(2)乘 除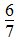
(3)减 乘 除 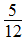
第3题
(1)×
(2)√
(3)×
(4)×
(5)√
第5题

第6题
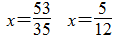
第7题
分析:本题考查了学生对分数的意义的理解及思维能力。解答此类问题,要先理清已知条件之间的关系,再根据每个算式提出相应的问题。(1)1200×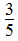 ,在题中找相应的已知条件,知道1200是“原计划种树的棵数,”
,在题中找相应的已知条件,知道1200是“原计划种树的棵数,”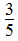 “是第二次种了原计划的
“是第二次种了原计划的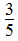 ”,由此可知“1200×
”,由此可知“1200×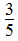 ”就是原计划种树棵数的
”就是原计划种树棵数的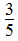 ,也就是第二次种树的棵数。因此,提出的问题是“第二次种了多少棵树?”(2)1200×
,也就是第二次种树的棵数。因此,提出的问题是“第二次种了多少棵树?”(2)1200×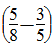 ,已知“1200”是原计划种树的棵数,“
,已知“1200”是原计划种树的棵数,“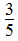 ”是第二次种了原计划的
”是第二次种了原计划的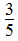 ,“
,“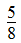 ”是第一次种了原计划的
”是第一次种了原计划的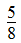 “
“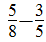 ”是第一次比第二次多种了原计划的几分之几?那么“1200×
”是第一次比第二次多种了原计划的几分之几?那么“1200×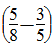 ”就是求第一次比第二次多种的棵数?因此,提出的问题是:第一次比第二次多种了多少棵树?(3)1200×
”就是求第一次比第二次多种的棵数?因此,提出的问题是:第一次比第二次多种了多少棵树?(3)1200×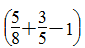 ,鉴于对前两题的分析可知,“
,鉴于对前两题的分析可知,“ ”是第一次和第二次一共种的棵数是原计划的几分之几。“
”是第一次和第二次一共种的棵数是原计划的几分之几。“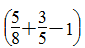 ”是求实际比原计划多种了几分之几。由此可知“1200×
”是求实际比原计划多种了几分之几。由此可知“1200×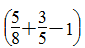 ”就是求实际比原计划多种了多少棵树。因此,提出的问题是:实际比原计划多种了多少棵树?
”就是求实际比原计划多种了多少棵树。因此,提出的问题是:实际比原计划多种了多少棵树?
解答:(1)第二次种了多少棵树?…………3分
(2)第一次比第二次多种了多少棵树?…………3分
(3)实际比原计划多种了多少棵树?…………3分
第8题
8000×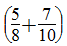 =10600(套)
=10600(套)
第9题
1200×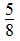 -1200×
-1200×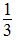 =350(kg)
=350(kg)
第10题
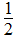 ×25×4=50(kg)
×25×4=50(kg)
第11题
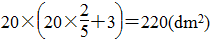
第12题
分析:本题考查了学生将分数计算与探索规律相结合的能力,以及对分数单位知识的掌握。针对此题,可以先找出所给分数分母的所有因数,再用所给分数分母的任意两个因数的和或差与所给分数的分母的乘积作分母,分子则依次是这两个因数,这样就可以得到几个分子是1的分数的和或差。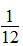 , 12的因数有1,2,3,4,6,12。那么,
, 12的因数有1,2,3,4,6,12。那么,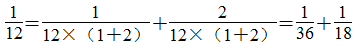
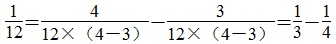 等。
等。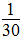 ,30的因数有1,2,3,5,6,10,15,30。那么,
,30的因数有1,2,3,5,6,10,15,30。那么,
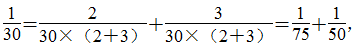 ,
,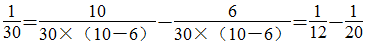 等。
等。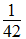 ,42的因数有1,2,3,6,7,14,21,42。那么
,42的因数有1,2,3,6,7,14,21,42。那么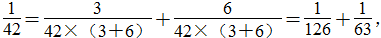
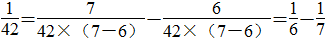 等。以上只是各举出两个例子,可以在分母的因数当中任意选择,答案不唯一。
等。以上只是各举出两个例子,可以在分母的因数当中任意选择,答案不唯一。
解答:(答案不唯一)
 …………(2分)
…………(2分)
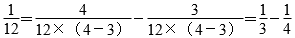 …………(1分)
…………(1分)
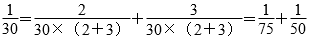 …………(2分)
…………(2分)
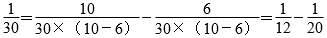 …………(1分)
…………(1分)
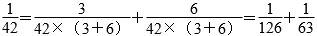 …………(2分)
…………(2分)
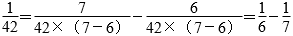 …………(2分)
…………(2分)
