西南师大版●六年级数学（下册）

第一题

1.14.13　15.42　2.260　2700　3.96　4.4　5.15.7　6.37.68　

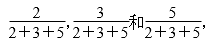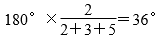
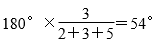
7. 分析：方法一：三角形的内角和是180°，根据一个三角形的三个内角的度数之比是2：3：5可知，三角形三个内角的度数分别占了三角形内角和的用乘法可分别求出各个内角的度数，再根据三角形的分类可确定是什么三角形．即 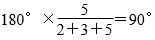。因为这个三角形有一个角是直角，所以这个三角形是直角三角形。
  解答：36°、54°、90°，直角。………（4分）

分析：方法二：本题还可列方程解答，设三角形的三个内角的度数分别为2x，3x和5x，可列方程为2x＋3x＋5x＝180°，解得x＝18°，所以2x＝36°，3x＝54°，5x＝90°，这个三角形是直角三角形。

解答：36°  54°  90°  直角 …………（4分）

第二题

1.×　2.√　3.×　

第三题

1.C　2.C　3.A　4.C　5.B　6.C

第五题

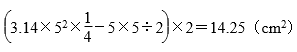
第六题

1，2　10，2　7，5

第七题

2.3.14×（10²－5²）×20＝4710（盆）  3．3.14×1.2×1×200＝753.6（m²）

4．3.14×6²×2.5×3÷（3.14×5²）＝10.8（cm）

5．分析：方法一：根据梯形的面积公式可先求出这个梯形的上底AD的长度是：45×2÷6－10＝5（厘米），由此可以利用三角形的面积公式求出三角形ABD的面积是：5×6÷2＝15（平方厘米），则三角形ABE的面积是15－5＝10（平方厘米），因为三角形ABC的面积是10×6÷2＝30（平方厘米），由此即可得出三角形BCE的面积是30－10＝20（平方厘米）。

解答：分步列式：

AD的长度是：45×2÷6－10＝5（厘米）……………（1分）

三角形ABD的面积是：5×6÷2＝15（平方厘米）………………（2分）

三角形ABE的面积是15－5＝10（平方厘米）…………（3分）

三角形ABC的面积是10×6÷2＝30（平方厘米）………………（5分）

所以三角形BCE的面积是30－10＝20（平方厘米）………………（7分）

答：阴影部分的面积是20平方厘米。……………（8分）

综合列式：10×6÷2－[（45×2÷6－10）×6÷2－5]………………（4分）

＝20（平方厘米）……………（7分）

答：阴影部分的面积是20平方厘米。…………（8分）

分析：方法二：通过观察可知，△ABC＋△DBC＋△AED－梯形面积＝阴影部分的面积。

解答：10×6×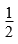×2＋5－45…………（4分）

    ＝20（平方厘米）……………（7分）

    答：阴影部分的面积是20平方厘米。………（8分）