北京版●六年级数学（下册）

第1题

10米²　62.8米²　188.4厘米²　

第2题

(1)A　(2)A　(3)C

第3题

314÷(3.14×2×5)＝10(厘米)

第4题

(1)251.2　(2)1256　(3)圆柱　4　5

第5题

12.56÷3.14÷2＝2(cm)

3.14×2²×2＋12.56×8＝125.6(cm²)

第6题

3.14×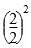×2＋3.14×2×1.5＝15.7(cm²)

第7题

分析：加工圆柱形薯片盒，就需要各个面都有，所以需要计算2个底面和1个侧面的面积之和，也就是求圆柱形薯片盒的表面积，即圆柱形薯片盒的表面积＝2×底面积＋侧面积＝（8÷2）²×3.14×2＋8×3.14×20＝602.88（cm²）。

解答：（8÷2）²×3.14×2＋8×3.14×20………………（2分）

＝4²×3.14×2＋8×3.14×20…………………………（4分）

＝100.48＋502.4…………………………（6分）

＝602.88（cm²）…………………………（7分）

答：做一个这样的薯片盒，至少需要602.88 cm²的纸板。…………（8分）

第8题

分析：求至少还需要多少平方厘米的纸板，实际上就是求底面周长是12.56 cm，高是18.84 cm的圆柱的底面积。

解答：12.56÷3.14÷2＝2(cm) ………………（3分）

3．14×2²＝12.56(cm²) ………………（7分）

答：至少还需要12.56平方厘米的纸板。………………（8分）

第9题

长方体　圆柱

长方体的表面积：(15×30＋15×50＋30×50)×2＝5400(cm²)

圆柱的表面积：3.14×6×10＋3.14×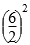×2＝244.92(cm²)

第10题

8÷2＝4(dm)

3.14×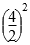×2＝25.12(dm²)

(16.56－4)×8＋25.12＝125.6(dm²)

第11题

分析：(1)把木棒沿横截面锯成2段，增加2个底面的面积；锯成3段，增加4个底面的面积，增加的表面积是125.6 cm²，所以木棒的底面积为125.6÷4＝31.4(cm²)。

(2)把木棒沿横截面锯成8段，要锯8－1＝7(次)，每锯1次增加2个底面，所以锯7次增加7×2＝14(个)底面。14个底面的面积是31.4×14＝439.6(cm²)。

(3)由“一个圆柱的高被截去5 cm后，圆柱的表面积减少了31.4 cm²”可知，31.4 cm²是截去圆柱的侧面积，可推出圆柱的底面周长为31.4÷5＝6.28(cm)，可得原来圆柱的侧面积为6.28×20＝125.6(cm²)。因为底面周长为6.28 cm，所以底面半径为6.28÷3.14÷2＝1(cm)，可求出圆柱的底面积为3.14×1²×2＝6.28(cm²)，原来圆柱的表面积为31.4÷5×20＋3.14×(31.4÷5÷3.14÷2)²×2＝131.88(cm²)。

解答：(1)①4………………（1分）　②4　31.4………………（3分）

(2)(8－1)×2＝14(个) ………………（8分）

31.4×14＝439.6(cm²)

(3)31.4÷5×20＋3.14×(31.4÷5÷3.14÷2)²×2＝131.88(cm²) …………（16分）