智慧广场 - 精版答案
第1题
6种
第2题
6种
第3题
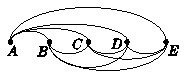
4+3+2+1=10(种)
第4题
6种
第5题
可以得到10个不同的积,分别是24、40、32、16、15、12、6、20、10、8。
第6题
分析:(1)用A、B、C、D、E、F分别代表6名同学,从6名同学中选出2名同学,根据图示可以得出:如果其中1名同学是A,A和其他人有5种组合方法,分别是A、B,A、C,A、D,A、E,A、F;如果其中1名同学是B,B和剩下的人有4种组合方法,分别是B、C,B、D,B、E,B、F;如果其中1名同学是C,C和剩下的人有3种组合方法,分别是C、D,C、E,C、F;如果其中1名同学是D,D和剩下的人有2种组合方法,分别是D、E,D、F;如果其中1名同学是E,E和剩下的人有1种组合方法,是E、F。则一共有5+4+3+2+1=15(种)组合方法,即有15种不同的选法。
(2)根据上题的解题方法可知,每两名同学比赛一场,一共要比赛9+8+7+6+5+4+3+2+1=45(场)。
解答:(1)5+4+3+2+1=15(种)……(6分)
(2)9+8+7+6+5+4+3+2+1=45(场)……(12分)
