1．图形的认识与测量 - （2）立体图形
第1题
（1）C （2）B （3）A （4）A
第2题
（1）× （2）× （3）× （4）× （5）√
第3题
（1）27.2 30 10.8
（2）62.8 102.05 78.5
（3）75.36 25.12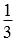 
第4题
3.14×（5÷2）2＝19.625（平方米）
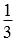×19.625×3.6＝23.55（立方米）
第5题
9÷3＝3（分米）
表面积：3×3×6＝54（平方分米）
体积：3×3×3＝27（立方分米）
第6题
3.14×（6÷2）2×18×2＝1017.36（立方厘米）＝1017.36（毫升）
1017．36>1000，能装下。
第7题
3.14×（2÷2）2×5×12×3÷[3.14×（10÷2）2 ]＝7.2（厘米）
第8题
表面积：20×20×5＝2000（平方厘米）
3.14×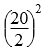
＝314（平方厘米）
20×3.14÷2×20＝628（平方厘米）
2000＋314＋628＝2942（平方厘米）
体积：20×20×20＋3.14×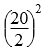×20÷2＝11140（立方厘米）
第9题
分析：要求这个水管每分钟水的流量，就是求这个圆柱的体积，求圆柱的体积就要知道圆柱的底面积和高。已知水管外直径和管壁的厚度可以求出内直径，进而求出半径，求出圆柱的底面积。水管中的水流速度是每秒8厘米，1分钟等于60秒，60×8＝480（厘米），一分钟流480厘米，就是这个圆柱的高。已知圆柱的底面积和高就能求出圆柱的体积了。
解答：
10÷2＝5（厘米）
5－0.5＝4.5（厘米）
3.14×4.52×8×60＝30520.8（立方厘米）
30520.8立方厘米＝30520.8毫升＝30.5208升
第10题
分析：这道题的突破口是求瓶子倒置时空余部分的容积。瓶子倒置时空余部分的高度是25－18＝7（厘米），又因为瓶子正放时400毫升油的油面高14厘米，所以瓶子倒置时空余部分的高7厘米对应装油200毫升。因此，这个瓶子的容积是400＋200＝600（毫升）。
解答：
25－18＝7（厘米）
14÷7＝2
400÷2＝200（毫升）
400＋200＝600（毫升）