2.长方体和正方体的表面积 - (3)正方体的表面积
第1题
(1)216
(2)4
(3)4
第2题
2.5×2.5×6=37.5(m2)
第3题
分析:
在一个大正方体上挖去一个棱长是1cm的小正方体,求大正方体的表面积会发生怎样的变化,需要看在哪个位置挖。图A是在大正方体的上面挖的小正方体,就使大正方体的表面积增加了小正方体的4个面,如图: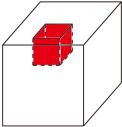 (把图A 的大正方体增加的4个面涂上红色,表示增加的面)。图B是沿着大正方体在棱上挖的小正方体,大正方体的表面积就增加了小正方体的2个面,如图:
(把图A 的大正方体增加的4个面涂上红色,表示增加的面)。图B是沿着大正方体在棱上挖的小正方体,大正方体的表面积就增加了小正方体的2个面,如图: (把图B的大正方体增加的2个面涂上红色,表示增加的面)。而图C是沿着大正方体在顶点上挖的小正方体,大正方体的表面积没变,如图:
(把图B的大正方体增加的2个面涂上红色,表示增加的面)。而图C是沿着大正方体在顶点上挖的小正方体,大正方体的表面积没变,如图: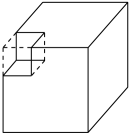 。
。
解答:
(1)C
(2)B
(3)A
第4题
分析:
用三个棱长相等的正方体拼成一个长方体,一共减少了4个正方体的面,如图: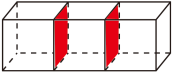 (画三个一样的正方体,拼接的面涂上红色),根据已知表面积减少了100cm2,能先求出一个面的面积:100÷4=25(cm2),再求出正方体的表面积:25×6=150(cm2)。
(画三个一样的正方体,拼接的面涂上红色),根据已知表面积减少了100cm2,能先求出一个面的面积:100÷4=25(cm2),再求出正方体的表面积:25×6=150(cm2)。
解答:
分步列式:
100÷4=25(cm2)……(3分)
25×6=150(cm2)……(4分)
答:每个正方体的表面积是150cm2。……(1分)
或综合列式:100÷4×6=150(cm2)……(7分)
答:每个正方体的表面积是150cm2。……(1分)
第5题
(6×4+2×4+6×2)×2+3×3×4=124(cm2)
第6题
分析:
(1)三面涂色的小正方体在大正方体的8个顶点处,如图: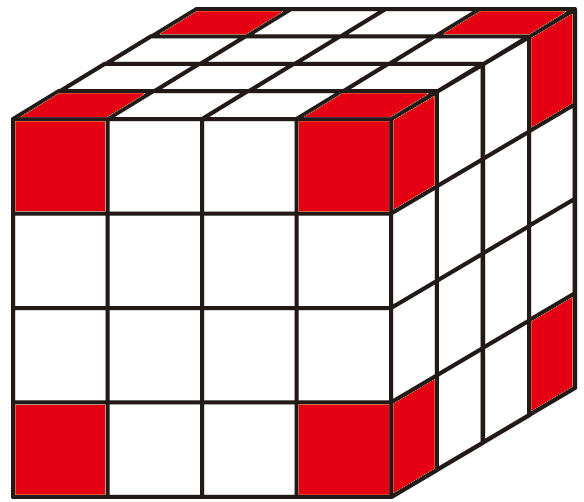 (画由64个小正方体拼成的大正方体,8个顶点处的小正方体的面涂成红色)。
(画由64个小正方体拼成的大正方体,8个顶点处的小正方体的面涂成红色)。
(2)两面涂色的小正方体在大正方体的12条棱上,每条棱上有两个,如图: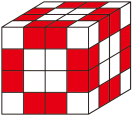 (画由64个小正方体拼成的大正方体,每条棱上中间的2个小正方体的面涂成红色)。
(画由64个小正方体拼成的大正方体,每条棱上中间的2个小正方体的面涂成红色)。
(3)一面涂色的小正方体在大正方体的6个面上,如图: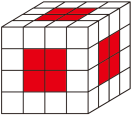 (画由64个小正方体拼成的大正方体,每个面正中间的4个小正方体的面涂成红色)。
(画由64个小正方体拼成的大正方体,每个面正中间的4个小正方体的面涂成红色)。
(4)没有涂红色的小正方体在大正方体的中心部分,眼睛见不到,但可以求出来,用64个小正方体减去涂红色的小正方体就是没有涂红色的小正方体。
解答:
(1)8
(2)2 24
(3)4 24
(4)56 8
