4.组合图形的面积 - （1）组合图形的面积
第2题
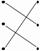
第3题
分析：（1）由图可知，三个图形的高是一样的，平行四边形的面积是4h，三角形的面积是8h÷2＝4h，梯形的面积是（2＋6）h÷2＝4h，所以三个图形的面积一样大。
（2）由题意可知，三个长方形是完全相同的，甲的面积正好是长方形的一半；乙的底是长方形的长，它的高是长方形的宽，它的面积就是长方形的一半；丙的底是长方形的宽，高是长方形的长，它的面积也是长方形的一半，所以这三个图形的面积一样大。
解答：(1)D (2)D
第4题
10×10＋10×4÷2＝120(m2)
第5题
分析：（1）用分割法求：先将图形分割成三部分，即两个同样大的梯形和一个长方形，然后分别求出两个梯形的面积和长方形的面积，最后把三个图形的面积相加。
解答：（6－1.5）÷2＝2.25（cm）…………………… （1分）
(2＋2.25)×2÷2×2＝8.5（cm2）……………………（2分）
6×（4－2）＝12（cm2）……………………（2分）
8.5＋12＝20.5（cm2）……………………（1分）
（2）用添补法求：先连线，使原图形成为一个完整的长方形，连线后的图形中间的部分是个梯形，然后分别求出长方形的面积和梯形的面积，最后再相减，即可求出图形的面积。
解答：6－2－2＝2（cm）……………………（3分）
6×4－（1.5＋2）×2÷2＝20.5（cm2）……………………（3分）
第6题
(1) 分析：辅助线把原图形分成一个梯形和一个长方形，先分别求出梯形的面积和长方形的面积，再相加，即可求出原图形的面积。
解答：(3＋4)×(4－2)÷2＋4×2＝15(dm2)
(2) 分析：辅助线把原图形分成一个梯形和一个长方形，先分别求出梯形的面积和长方形的面积，再相加，即可求出原图形的面积。
解答: (2＋4)×(4－3)÷2＋3×4＝15(dm2)
(3) 分析：辅助线把正方形缺的部分补上了，只要先分别求出原正方形的面积和三角形的面积，再相减，即可求出图形的面积。
解答:4×4－(4－3)×(4－2)÷2＝15(dm2)
第7题
6×6＋4×4－(6＋4)×6÷2＝22(cm2)
第8题
分析：此题可用剔除法解决。长方形中“Y”以外有三部分，分别是一个三角形和两个梯形。从长方形的面积中剔除一个三角形的面积和两个梯形的面积，即是“Y”的面积。
解答： 6×8－3×（8－4）÷2－（4＋8）×2÷2×2……………………（5分）
＝48－6－24……………………（2分）
＝18（cm2）……………………（2分）
第9题
分析：在图中作两条辅助线把阴影部分分成三部分，即两个完全相同的长方形和一个正方形，如图所示：
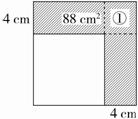
用阴影部分的面积减去①的面积，所得的差再除以2就是其中一个长方形的面积，长方形的面积再除以它的宽4 cm，可得到长方形的长，即原正方形的边长。
解答：（88－4×4）÷2÷4……………………（6分）
＝9（cm）……………………（2分）
9×9＝81（cm2）……………………（3分）