六年级数学(下册) - 练习九
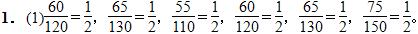
(2)表示每千瓦时的电费。
(3)成正比例关系,因为每千瓦时的电费一定,也就是电费与相应的用电量的比值一定。

(2)正方体的表面积=棱长的平方×6,正方体的表面积与棱长的平方的比值一定,但与棱长的比值不固 定,所以正方体的表面积与它的棱长不成正比例关系。
(3)一个人的身高与他的年龄没有直接关系,所以一个人的身高与他的年龄不成正比例关系。

(5)总页数=已读的页数+未读的页数,所以未读的页数与已读的页数不成正比例关系。

(2)它是一条从原点出发的射线。
(3)约7.33 L
4.

5.(1)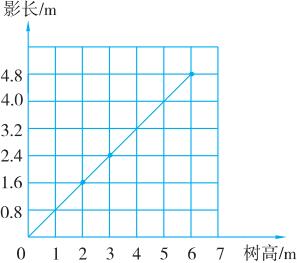
图象是一条从原点出发的射线。
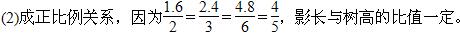
6.

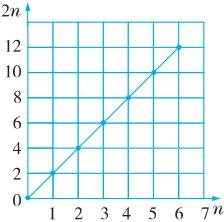
(1)2n表示自然数中的偶数。
(2) 
(发现略)
7.

(1) 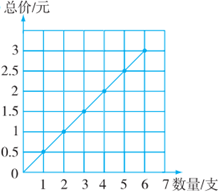
(2)3.5元
(3)4倍
8.9×6=54(m2)
900×600=540000(cm2)=54(m2)
1800×300=540000(cm2)=54(m2)
3600×150=540000(cm2)=54(m2)
所需地砖数量与每块地砖的面积成反比例关系,因为教室的面积一定,而所需地砖数量与每块地砖的面积的乘积都等 于教室的面积54 m2。
9.250×1200=300000(mL)=300(L)
500×600=300000(mL)=300(L)
750×400=300000(mL)=300(L)
1500×200=300000(mL)=300(L)
因为每瓶容量×所装瓶数=这批醋的体积(体积一定,都是300 L),所以所装瓶数与每瓶容量成反比例关系。
10.

11.(1)因为每天的平均用煤量×使用天数=煤的数量(一定),所以使用天数与每天的平均用煤量成反比例关系。
(2)因为每组的人数×组数=全班的人数(一定),所以组数与每组的人数成反比例关系。
(3)因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积与高成反比例关系。
(4)因为种黄瓜的面积与种西红柿的面积的和一定,而它们的乘积不一定,所以种黄瓜的面积与种西红柿的面积不成反比 例关系。
(5)因为每包的册数×包数=书的总册数(一定),所以包数与每包的册数成反比例关系。
12.(1)组装的手机总数=pt
(2)分析:因为500×24=12000,600×20=12000,800×15=12000,
1000×12=12000,1200×10=12000,说明p与t的积一定
(都是12000),所以p与t成反比例关系。
解答:p与t成反比例关系。
(3)500×24÷8=1500(部)
13.(1)260×5=1300(千米)
(2)成反比例关系,tv=1300。
(3)1300÷325=4(时)
14.(1)斑马和长颈鹿的奔跑路程和奔跑时间都成正比例关系。
(2)从图象中可知,斑马18分钟大约跑22 km;长颈鹿18分钟大约跑14 km。(答案不唯一,合理即可)
(3)斑马跑得快。
15*.(1)反 (2)正 (3)正
16*.分析:长×宽=长方形的面积,长用x表示,宽用y表示,面积是36 cm2,
由此得出xy=36,y与x的乘积一定,所以y与x成反比例关系。
要把y与x的关系用图象表示出来,可以先根据长方形的面积列举出x、y的几组数据,再在图中描点连线。
解答:y与x成反比例关系。
列举数据:

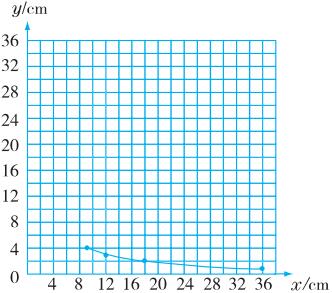
xy=36的图象不是一条直线,而是一条曲线。
