六年级数学(下册) - 练习十八
1.(1)× (2)√ (3)×
2.km m2 kg L
3.略
4.第一组中两个图形的面积相等,周长不相等;第二组中两个图形的周长相等,面积不相等。
5.能画无数个与给定的平行四边形面积相等的图形。
发现:只要画出的图形是由10个小方格拼成的,就与给定的平行四边形的面积相等。
6.分析:等底等高的三角形的面积是平行四边形面积的一半。
解答:30÷2=15(cm2)
7.略
8.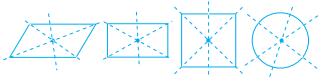
画一条直线把上面每个图形分成面积相等的两部分,每个图形都有无数种画法。
发现:经过每个图形的中心点的任意一条直线都能把这个图形分成面积相等的两部分。
9.左图是从左面看到的;中图是从上面看到的;右图是从正面看到的。
10.(1)F面 (2)略 (3)至少要量出3条不同长度的边的长度。
11.(6÷2)×(6÷2)×(6÷2)=27(个)
2×2×6×27-6×6×6=432(cm2)
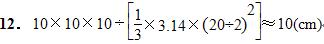
13.提示:用小正方体代替货物实际摆摆看,发现这堆货物可能有10箱,也可能有9箱。
14.表面积:20×20×5+3.14×20×20÷2+3.14×(20÷2)2=2942(cm2)
体积:20×20×20+3.14×(20÷2)2×20÷2=11140(cm3)
15*.(1)一共有10个正方体,它的体积是5×5×5×10=1250(cm3)。
(2)2个 (3)2个 (4)6个
16*.分析:正方形的边长正好是四分之一圆的半径。已知正方形的面积是10 cm2,那么圆的半径的平方也就是10 cm2。根据S=πr2即可求出整个圆的面积,再求四分之一圆的面积。
解答:
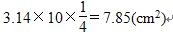
17*.分析:在围成的长方体的表面糊一层纸,要让所用的纸最多,就是让这个长方体的表面积最大。经尝试,当围成长、宽、高相等的长方体,即正方体时,表面积最大,所用的纸最多。
解答: 24÷12=2(cm)
当围成一个棱长是2 cm的正方体框架时,在它的表面糊一层纸,所用的纸最多。
