3.三角形的分类 - 精版答案
第1题
略
第2题
（1）C
（2）分析：一个三角形有三个角，三个角的和为180°，设这三个角分别为A、B、C，由题中已知其中两个角的和等于第三个角，推出：
A＋B＋C＝180°
A＋B＝C
C＋C＝180°
C＝180°÷2
C＝90°
由此可推断出这个三角形是直角三角形。
解答：B
（3）分析：要想求这个等腰三角形的周长，首先要判定它的腰长和底边长各是多少。根据“三角形任意两边之和大于第三边”推导。
第一种情况：腰长是4cm，底边长是8cm。
4＋4＝8，4＋8＝12＞4，4＋8＝12＞4，
不符合围成三角形的条件，所以这样的等腰三角形不存在。也就是腰长是4cm，底边长是8cm的等腰三角形不存在。
第二种情况：腰长是8cm，底边长是4cm。
8＋8＝16＞4，4＋8＝12＞8，4＋8＝12＞8，
符合围成三角形的条件，可以判定这个等腰三角形的腰长是8cm，底边长是4cm，所以周长是8＋8＋4＝20（cm）或8×2＋4＝20（cm）。
解答：B
第3题
（1）×
（2）分析：题中给出等腰三角形的周长是20cm，也就是说这个等腰三角形的腰长是5cm，底边长是10cm，根据“三角形任意两边之和大于第三边”判断这样的等腰三角形是不存在的。所以这道题说得不对。
解答：×
（3）√
（4）分析：题中说出了两种情况，这两种情况都没有明确说明等腰三角形腰的准确值。
①假设第一个等腰三角形的腰长是3cm，底边长是7cm，根据“三角形任意两边之和大于第三边”“3＋3＜7”说明这个等腰三角形不存在，假设不成立。
②假设第一个等腰三角形的腰长是7cm，底边长是3cm，那么它的周长是7＋7＋3＝17（cm）或7×2＋3＝17（cm），题中的叙述是正确的。
③假设第二个等腰三角形的腰长是3cm，底边长是4cm，那么它的周长是3＋3＋4＝10（cm）或3×2＋4＝10（cm）。
④假设第二个等腰三角形的腰长是4cm，底边长是3cm，那么它的周长是4＋4＋3＝11（cm）或4×2＋3＝11（cm），题中第二个等腰三角形的叙述也是正确的。
解答：√
第4题
分析：解决此题可动手用量角器量一量，通过测量，第一个角为钝角；第二个角为直角，根据定义“有一个角是钝角的三角形叫做钝角三角形” “有一个角是直角的三角形叫做直角三角形”可判定（1）为钝角三角形，（2）为直角三角形。
解答：（1）钝角三角形 （2）直角三角形（每空3分）
第5题
略
第6题
90÷3＝30（cm）
第7题
分析：要在一个三角形中画一条线段，将其分成两个直角三角形。首先要明确“有一个角是直角的三角形叫做直角三角形”，然后动手操作尝试，从三角形的一个顶点到它的对边做一条垂线段，这样画一条线段就可将一个三角形分成两个直角三角形。
解答：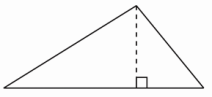
……（4分） 
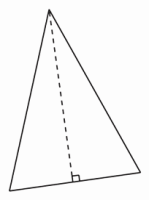……（4分）
第8题
略
第9题
分析：此题可先用量角器量一量平行四边形角的度数，会发现这个平行四边形中有两个钝角，两个锐角。要想把这个平行四边形分成两个完全一样的锐角三角形，只要连接两个钝角的顶点即可。同样道理，要想把这个平行四边形分成两个完全一样的钝角三角形，只要连接两个锐角的顶点即可。
解答：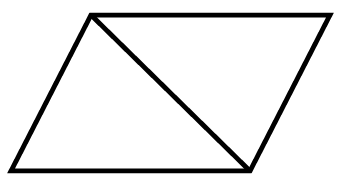
第10题
（24－10）÷2＝7（m）
第11题
分析：此题的基本图形是
。
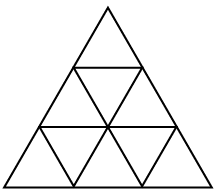
（1）由1 个基本三角形组成的三角形有（9）个。
（2）由4个基本三角形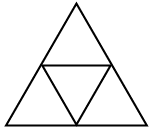
组成的三角形有（3）个。
（3）由9个基本三角形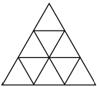
组成三角形有（1）个。
（4）把分类统计的三角形个数加起来，图中共有（13）个三角形。
解答：（1）9 （2）3 （3）1 （4）13 （每空2分）
（5）分析：此题的基本图形是。
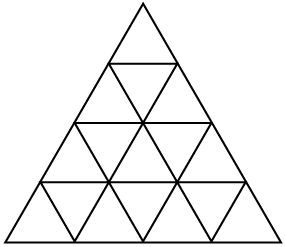
①由1个基本三角形组成的三角形有（16）个。
②由4个基本三角形组成的三角形有（7）个。
③由9个基本三角形组成的三角形有（3）个。
④由16个基本三角形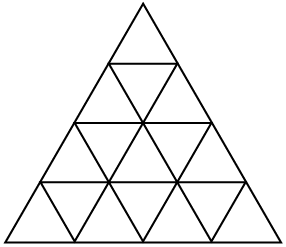
组成的三角形有（1）个。
⑤把分类统计的三角形个数加起来，图中共有（27）个三角形。
解答：27个……（2分）