4.三角形的内角和 - 精版答案
第1题
(1)180°
(2)直角
(3)相等 60°
(4)30° 30°
(5)70° 锐角 等腰
第2题
分析:解决此题,首先要确定这个图形是什么三角形,然后再根据三角形的特点判断题中的说法是否正确。
(1)此三角形是钝角三角形,其中一个角是钝角,另外两个角都是锐角,钝角是大于90°而小于180°的角,且三角形的内角和是180°,可设这个钝角为91°,则剩下两个锐角和为180°-91°=89°,89°<90°,所以此题的说法是不正确的。
(2)此三角形是直角三角形,其中一个角是直角,另外两个角都是锐角,由三角形内角和是180°推出:直角三角形的两个锐角之和=180°-90°=90°,所以此题的说法是正确的。
(3)因为只要是三角形它的内角和就是180°,把一个三角形分成两个三角形后每个三角形的内角和还是180°,所以此题中的说法是不正确的。
(4)因为此三角形是等边三角形,等边三角形三条边相等,三个角相等,都是60°。如图:
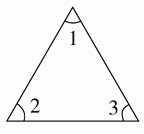
∠1=∠2=∠3=60°
∠1+∠2=60°+60°=120°>90°
∠1+∠3=60°+60°=120°>90°
∠2+∠3=60°+60°=120°>90°
所以此题中的说法是正确的。
解答:(1)× (2)√ (3)× (4)√(每空2分)
第3题
(1)73° (2)35° (3)134°
第4题
分析:要想知道这三块三角形纸板各是什么三角形,就要根据三角形内角和是180°先求出未知角的度数。再根据三角形三个角的度数去判断。
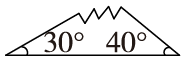
未知角的度数为:180°-30°-40°=110°或
180°-(30°+40°)=110°(钝角)
有一个角是钝角的三角形是钝角三角形。
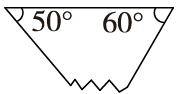
未知角的度数为:180°-50°-60°=70°或
180°-(50°+60°)=70°(锐角)
三个角都是锐角的三角形是锐角三角形。
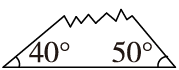
未知角的度数为180°-40°-50°=90°或
180°-(40°+50°)=90°(直角)
有一个角是直角的三角形是直角三角形。
解答:钝角三角形……(3分)
锐角三角形……(3分)
直角三角形……(3分)
第5题
略
第6题
分析:解决此题,可先动手画一画,再观察,从而找到解题方法。
折前图:
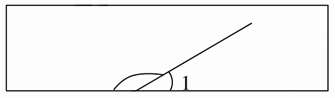
折前图中的大角和∠1组成了一个平角,平角是180°。
折后图:
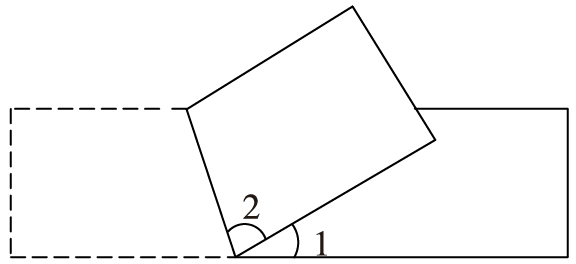
观察折后图与折前图可发现,∠2是重合的,即2∠2就是折前图中的大角。由此可推出:
2∠2+∠1=180°,∠1=30°,所以2∠2=180°-30°=150°,∠2=75°。
解答:∠1+∠2+∠2=180°……(4分)
30°+∠2+∠2=180°
∠2+∠2=150°……(1分)
∠2=75°……(2分)
