5.解决问题 - 精版答案
第1题
相等 相等 360°
相等 相等 360°
相等 相等 360°
第2题
分析：因为没有直接求多边形内角和的方法，所以就要根据三角形的内角和是180°来计算。因此，就要想办法将多边形分割成几个三角形。这样就能很快求出它们的内角和，
题中的四边形可分成2个三角形，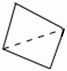
或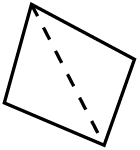
，由此推出四边形的内角和为180°×2＝360°。
题中的五边形可分成3个三角形（可从任意顶点作分割线），即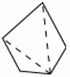
，由此推出五边形的内角和为180°×3＝540°。
题中的六边形可分成4个三角形（可从任意顶点作分割线），即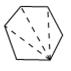
，由此推出六边形的内角和为180°×4＝720°。
由以上各图形的边数与对应的三角形的个数可填出如下表格：
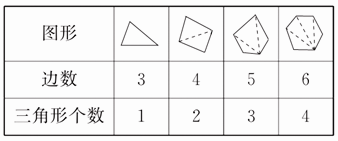
由上表推出：图形边数－2＝三角形个数。
根据此规律，可推出十二边形的内角和：
12－2＝10（个） 180°×10＝1800°
解答：
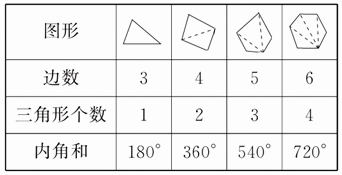
（每空1分）
12－2＝10（个）……（1分）
十二边形的内角和：180°×10＝1800°……（2分）
第3题
（1）分析：四边形的内角和＝（4－2）×180°＝2×180°＝360°。如图，已知四边形的三个内角的度数分别是120°、60°、60°，可推出∠1＝360°－120°－60°－60°＝120°。
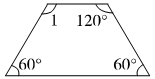
解答：∠1＝360°－60°×2－120°＝120°……（3分）
（2）分析：四边形的内角和＝（4－2）×180°＝2×180°＝360°。如图，已知四边形两个直角，另一个内角的度数为125°，可推出∠2＝360°－90°－90°－125°＝55°。
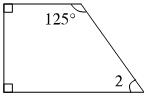
解答：∠2＝360°－90°×2－125°＝55°……（3分）
第4题
分析：一副三角板中的一个三角板是等腰直角三角形，它的两个锐角都是45°，另一个三角板中较小的锐角是30°，较大的锐角是60°。（1）如图所示，把三角板各个角的度数标出来，则∠1＝180°－30°－45°＝150°－45°＝105°或∠1＝180°－（30°＋45°）＝180°－75°＝105°。因为∠2＋∠1＝180°，∠1＝105°，所以∠2＝180°－∠1＝180°－105°＝65°。又因为45°＋∠3＝180°，所以∠3＝180°－45°＝135°。
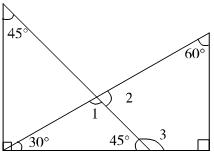
解答：∠1＝180－30°－45°＝105°……（3分）
∠2＝180°－∠1＝180°－105°＝75°……（3分）
∠3＝180°－45°＝135°……（3分）
第5题
（7－2）×180°＝900°
第6题
分析：由三角形的内角和＝（3－2）×180°＝180°，四边形的内角和＝（4－2）×180°＝360°，五边形的内角和＝（5－2）×180°＝540°，提出图形的内角和＝（边数－2）×180°，由此推出n边形的内角和是（n－2）×180°。
解答：（n－2）×180°