人教版●四年级数学（下册）

第一题

1.A　C　

2.C　

3.分析：根据“三角形任意两边之和大于第三边”进行判断。

（1）5cm，5cm，5cm是等边三角形，

5cm＋5cm＝10cm＞5cm,

5cm＋5cm＝10cm＞5cm,

5cm＋5cm＝10cm＞5cm,

能拼成三角形。

（2）5cm，1cm，7cm,

5cm＋1cm＝6cm＜7cm,

5cm＋7cm＝12cm＞1cm,

1cm＋7cm＝8cm＞5cm,

不能拼成三角形。

（3）2cm，3cm，4cm,

2cm＋3cm＝5cm＞4cm,

2cm＋4cm＝6cm＞3cm,

3cm＋4cm＝7cm＞2cm,

能拼成三角形。

所以不能拼成三角形的是B。

解答：B　

4.C　

5.分析：如图，最少用3个等边三角形可以拼成一个梯形。

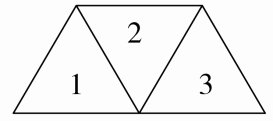
解答：A　

6.C　

7.分析：从两根9cm、两根4cm和两根2cm的小棒中任选三根围成一个等腰三角形，

可选取两根9cm和1根4cm的围成等腰三角形，周长为9＋9＋4＝22（cm）；

可选取两根9cm和1根2cm的围成等腰三角形，周长为9＋9＋2＝20（cm）；

可选取两根4cm和1根2cm的围成等腰三角形，周长为4＋4＋2＝10（cm）。

解答：B

8.分析：“如果以三角形ABC的BC边为底，那么三角形ABC的高是多少？”实际上就是从顶点A向对边BC做一条高，因为三角形ABC是钝角三角形，∠ABC是钝角，所以BC边上的高在三角形ABC外面。如图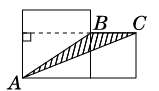，发现从顶点A向对边BC作的高与小正方形的边长相等，由此推出：如果以三角形ABC的BC边为底，那么三角形ABC的高与小正形的边长相等，即4cm。

解答：A

第二题

略

第三题

2.俄罗斯体育代表团　加拿大体育代表团

3.（11＋9）÷2＝10（枚）

第四题

1.分析：由图可知∠ACB＋80°＝180°，所以∠ACB＝180°－80＝100°，又由三角形内角和是180°，可得∠A＝180°－100°－38°＝42°。

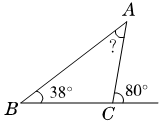
解答：因为∠ACB＋80°＝180°，所以∠ACB＝180°-80°＝100°。又因为∠A+∠B+∠ACB＝180°，所以∠A＝180°－∠B－∠ACB＝180°－100°－38°＝42°。

2.分析：由“已知AC＝BC”可知△ABC是一个等腰三角形，则两底角度数相同，即∠A＝∠B。又因为∠A＋∠B＋∠C＝180°，所以∠A＝∠B＝（180°－124°）÷2＝28°。

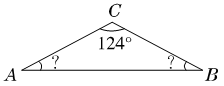
解答：∠A＝∠B＝（180°－124°）÷2＝28°

第五题

略

第六题

1.（50－18）÷2＝16（cm）

2.分析：等腰三角形中两个底角的度数相等，两底角的度数和为25°＋25°＝50°,根据“三角形的内角和是180°”可以推出顶角的度数＝180°－50°＝130°。

解答：

方法一：

  180°－25°－25°……（3分）

＝155°－25°……（2分）

＝130°……（2分）

方法二：

180°－（25°＋25°）……（3分）

＝180°－50°……（2分）

＝130°……（2分）

答：它的顶角的度数为130°。……（1分）

3.90°÷3＝30°　90°－30°＝60°　这块三角形菜地三个角的度数分别是90°、60°、30°。